樹

1.樹的概念和模型

樹：是一種非線性的數據結構，它是由n(n>=0)個有限結點組成一個具有層次關系的集合。把它 叫做樹是因為它看起來像一棵倒掛的樹，也就是說它是根朝上，而葉朝下的。

有一個特殊的結點，稱為根結點，根節點沒有前驅結點

除根節點外，其余結點被分成M(M>0)個互不相交的集合T1、T2、……、Tm，其中每一個集 合Ti(1<= i <= m)又是一棵結構與樹類似的子樹。每棵子樹的根結點有且只有一個前驅，可以 有0個或多個后繼

因此，樹是遞歸定義的。

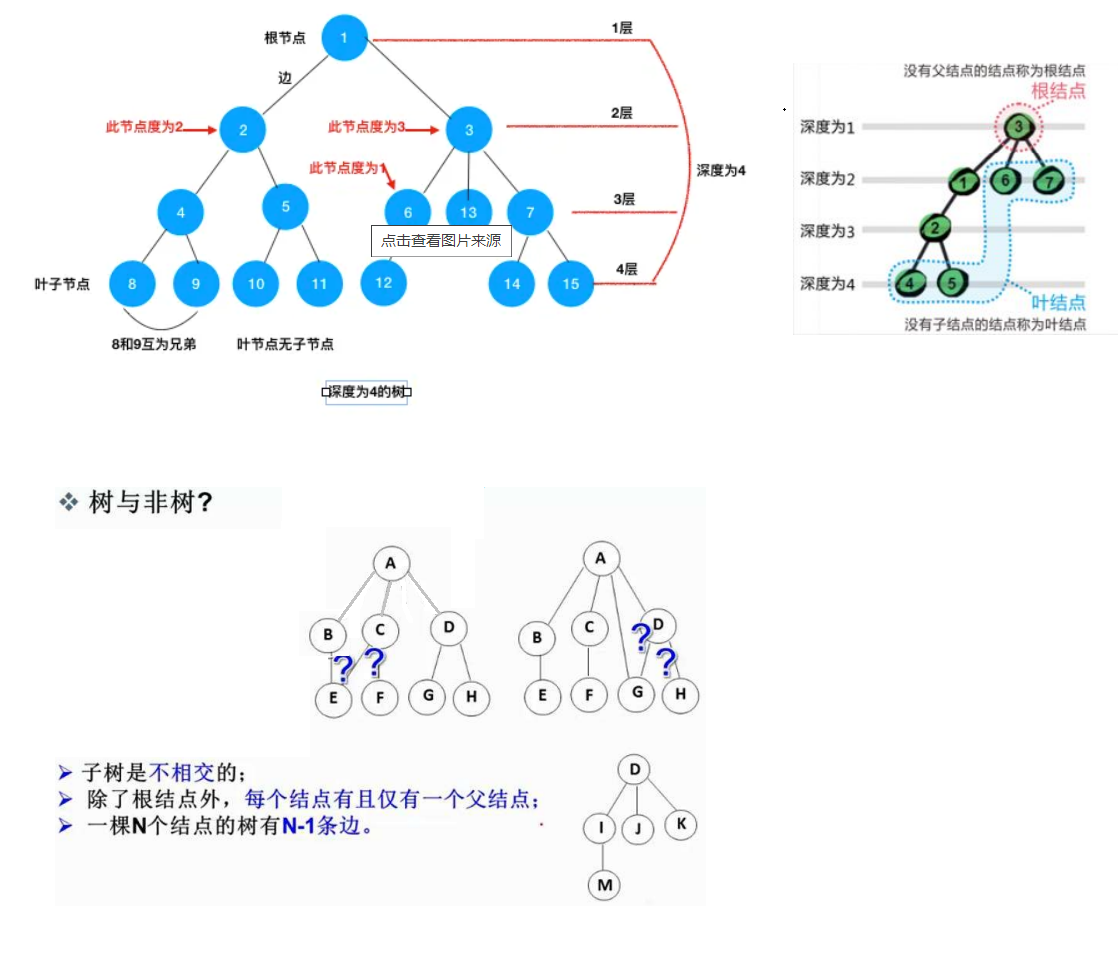
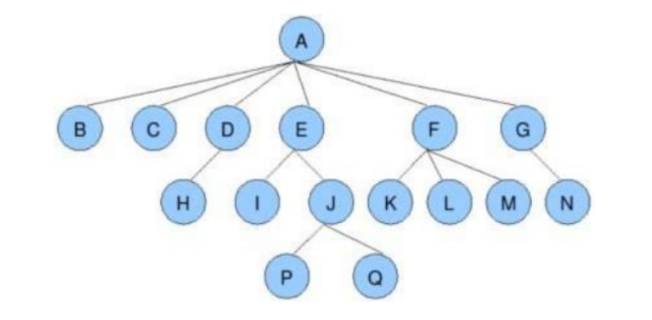
節點的度：一個節點含有的子樹的個數稱為該節點的度; 如上圖：A的為6

葉節點或終端節點：度為0的節點稱為葉節點; 如上圖：B、C、H、I…等節點為葉節點

非終端節點或分支節點：度不為0的節點; 如上圖：D、E、F、G…等節點為分支節點

雙親節點或父節點：若一個節點含有子節點，則這個節點稱為其子節點的父節點; 如上圖：A是B 的父節點

孩子節點或子節點：一個節點含有的子樹的根節點稱為該節點的子節點; 如上圖：B是A的孩子節點

兄弟節點：具有相同父節點的節點互稱為兄弟節點; 如上圖：B、C是兄弟節點

樹的度：一棵樹中，最大的節點的度稱為樹的度; 如上圖：樹的度為6

節點的層次：從根開始定義起，根為第1層，根的子節點為第2層，以此類推;

樹的高度或深度：樹中節點的最大層次; 如上圖：樹的高度為4

節點的祖先：從根到該節點所經分支上的所有節點;如上圖：A是所有節點的祖先

子孫：以某節點為根的子樹中任一節點都稱為該節點的子孫。如上圖：所有節點都是A的子孫

森林：由m(m>0)棵互不相交的多顆樹的集合稱為森林;(數據結構中的學習并查集本質就是 一個森林)

2.樹的表示

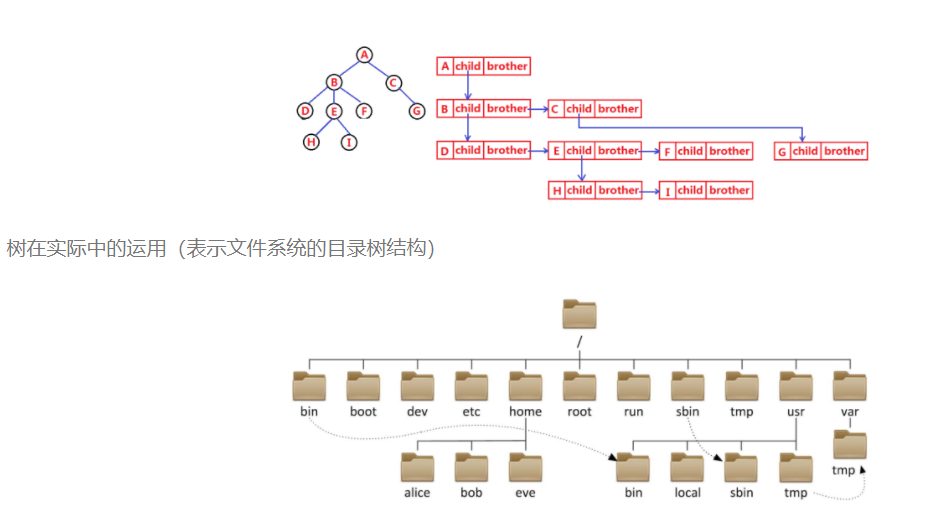
樹結構相對線性表就比較復雜了，要存儲表示起來就比較麻煩了，實際中樹有很多種表示方式， 如：雙親表示法，孩子表示法、孩子兄弟表示法等等。我們這里就簡單的了解其中最常用的孩子 兄弟表示法。

typedef int DataType;
struct Node
{
    struct Node* firstChild1;    // 第一個孩子結點
    struct Node* pNextBrother;   // 指向其下一個兄弟結點
    DataType _data;               // 結點中的數據域
};

二叉樹

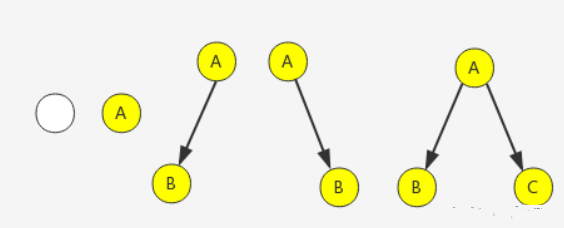
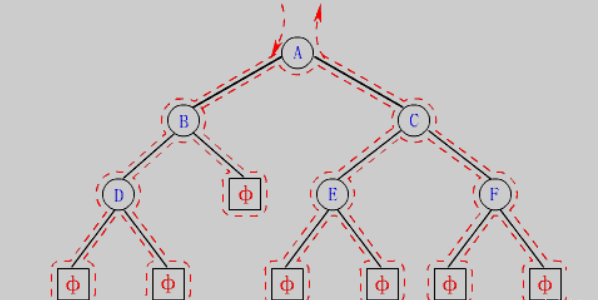
二叉樹：一棵二叉樹是結點的一個有限集合，該集合或者為空，或者是由一個根節點加上兩棵別稱為左子 樹和右子樹的二叉樹組成。 二叉樹的特點：

每個結點最多有兩棵子樹，即二叉樹不存在度大于2的結點。

二叉樹的子樹有左右之分，其子樹的次序不能顛倒。

1.特殊的二叉樹：

滿二叉樹：一個二叉樹，如果每一個層的結點數都達到最大值，則這個二叉樹就是滿二叉 樹。也就是說，如果一個二叉樹的層數為K，且結點總數是(2^k) -1 ，則它就是滿二叉樹。

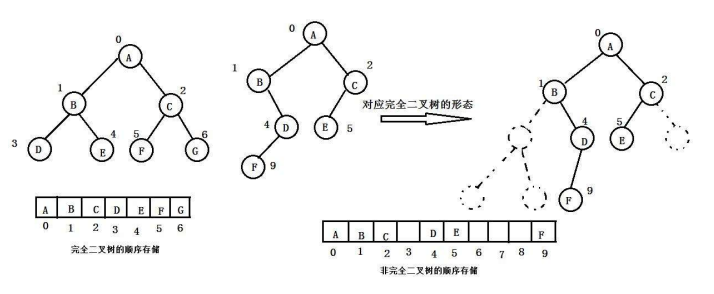
完全二叉樹：完全二叉樹是效率很高的數據結構，完全二叉樹是由滿二叉樹而引出來的。對 于深度為K的，有n個結點的二叉樹，當且僅當其每一個結點都與深度為K的滿二叉樹中編號 從1至n的結點一一對應時稱之為完全二叉樹。 要注意的是滿二叉樹是一種特殊的完全二叉樹。(假設樹的高度是h，前h-1層都是滿的，最后一層不滿，但最后一層從左往右都是滿的)

2.二叉樹的存儲結構

? 二叉樹一般可以使用兩種結構存儲，一種順序結構，一種鏈式結構。

(1)二叉樹的性質

若規定根節點的層數為1，則一棵非空二叉樹的第i層上最多有2(i-1) 個結點.

若規定根節點的層數為1，則深度為h的二叉樹的最大結點數是2h- 1.

對任何一棵二叉樹, 如果度為0其葉結點個數為 n0, 度為2的分支結點個數為 n2,則有n0=n2 +1

若規定根節點的層數為1，具有n個結點的滿二叉樹的深度，h=LogN

(2)順序存儲：

? 順序結構存儲就是使用數組來存儲，一般使用數組只適合表示完全二叉樹，因為不是完全二叉樹 會有空間的浪費。而現實中使用中只有堆才會使用數組來存儲，二叉樹順序存儲在物理上是一個數組，在邏輯上是一顆二叉樹。

(3)鏈式存儲：

? 二叉樹的鏈式存儲結構：用鏈表來表示一棵二叉樹，即用鏈來指示元素的邏輯關系。 通常的 方法是鏈表中每個結點由三個域組成，數據域和左右指針域，左右指針分別用來給出該結點左孩 子和右孩子所在的鏈結點的存儲地址 。鏈式結構又分為二叉鏈和三叉鏈，當前我們學習中一般都 是二叉鏈，后面課程學到高階數據結構如紅黑樹等會用到三叉鏈。

// 二叉鏈
struct BinaryTreeNode
{
   struct BinTreeNode* pLeft;   // 指向當前節點左孩子
   struct BinTreeNode* pRight; // 指向當前節點右孩子
   BTDataType _data; // 當前節點值域
}
// 三叉鏈
struct BinaryTreeNode
{
   struct BinTreeNode* pParent; // 指向當前節點的雙親
   struct BinTreeNode* pLeft;   // 指向當前節點左孩子
   struct BinTreeNode* pRight; // 指向當前節點右孩子
   BTDataType _data; // 當前節點值域
}；

3.二叉樹鏈式結構的遍歷

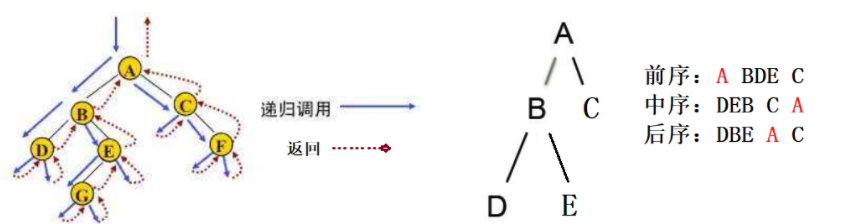
? 所謂遍歷(Traversal)是指沿著某條搜索路線，依次對樹中每個結點均做一次且僅做一次訪問。訪 問結點所做的操作依賴于具體的應用問 題。 遍歷是二叉樹上最重要的運算之一，是二叉樹上進行 其它運算之基礎。

前序/中序/后序的遞歸結構遍歷：是根據訪問結點操作發生位置命名 5

NLR：前序遍歷(Preorder Traversal 亦稱先序遍歷)——訪問根結點的操作發生在遍歷其左右子樹之前。

LNR：中序遍歷(Inorder Traversal)——訪問根結點的操作發生在遍歷其左右子樹之中 (間)。

LRN：后序遍歷(Postorder Traversal)——訪問根結點的操作發生在遍歷其左右子樹之后。

由于被訪問的結點必是某子樹的根，所以N(Node)、L(Left subtree)和R(Right subtree)又 可解釋為根、根的左子樹和根的右子樹。NLR、LNR和LRN分別又稱為先根遍歷、中根遍歷和后根 遍歷。

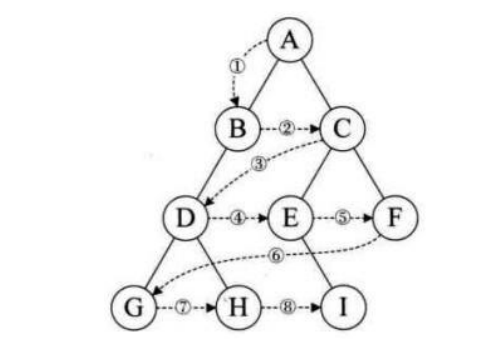
層序遍歷：除了先序遍歷、中序遍歷、后序遍歷外，還可以對二叉樹進行層序遍歷。設二叉樹的 根節點所在層數為1，層序遍歷就是從所在二叉樹的根節點出發，首先訪問第一層的樹根節點，然 后從左到右訪問第2層上的節點，接著是第三層的節點，以此類推，自上而下，自左至右逐層訪問樹的結點的過程就是層序遍歷。(廣度優先)

4.二叉樹實現的代碼

#include<stdio.h>
#include<stdlib.h>
#include<stdbool.h>

typedef char BTDataType;
typedef struct BinaryTreeNode
{
	struct BinaryTreeNode* left;
	struct BinaryTreeNode* right;
	BTDataType data;
}BTNode;
//樹一般不直接遍歷沒有意義，就前中后序遍歷
//分治遞歸算法
void PrevOrder(BTNode* root)//前序
{
	if (NULL == root)
	{
		printf("NULL ");
		return;
	}
	printf("%c ", root->data);
	PrevOrder(root->left);
	PrevOrder(root->right);
}
void InOrder(BTNode* root)//中序
{
	if (NULL == root)
	{
		printf("NULL ");
		return;
	}
	InOrder(root->left);
	printf("%c ", root->data);
	InOrder(root->right);
}
void PostOrder(BTNode* root)//后序
{
	if (NULL == root)
	{
		printf("NULL ");
		return;
	}
	PostOrder(root->left);
	PostOrder(root->right);
	printf("%c ", root->data);
}
//int size = 0;//方式一：定義全局變量（一般不用）
int TreeSize(BTNode* root)//求樹節點的個數
{
	//if (NULL == root)
	//{
	//	return;
	//}
	//++size;
	//TreeSize(root->left);
	//TreeSize(root->right);
	//return size;
	//方式二
	return root == NULL ? 0 : TreeSize(root->left) + TreeSize(root->right) + 1;
}
int TreeLeafSize(BTNode* root)//求葉子節點的個數
{
	if (NULL == root)
		return 0;
	if (NULL == root->left && NULL == root->right)
		return 1;
	return TreeLeafSize(root->left) + TreeLeafSize(root->right);
}
int main()
{
	BTNode* A = (BTNode*)malloc(sizeof(BTNode));
	A->data = 'A';
	A->left = NULL;
	A->right = NULL;
	BTNode* B = (BTNode*)malloc(sizeof(BTNode));
	B->data = 'B';
	B->left = NULL;
	B->right = NULL;
	BTNode* C = (BTNode*)malloc(sizeof(BTNode));
	C->data = 'C';
	C->left = NULL;
	C->right = NULL;
	BTNode* D = (BTNode*)malloc(sizeof(BTNode));
	D->data = 'D';
	D->left = NULL;
	D->right = NULL;
	BTNode* E = (BTNode*)malloc(sizeof(BTNode));
	E->data = 'E';
	E->left = NULL;
	E->right = NULL;
	A->left = B;
	A->right = C;
	B->left = D;
	B->right = E;
	PrevOrder(A);
	printf("\n");
	InOrder(A);
	printf("\n");
	PostOrder(A);
	printf("\n");
	printf("%d\n", TreeSize(A));
	printf("%d\n", TreeLeafSize(A));
	return 0;
}
//判斷樹是否是高度平衡的二叉樹。（一個二叉樹每個節點 的左右兩個子樹的高度差的絕對值不超過 1 。）
struct TreeNode {
	int val;
	struct TreeNode* left;
	struct TreeNode* right;
};
//求樹的最大深度
int maxDepth(struct TreeNode* root) {
	if (NULL == root)
		return 0;
	int leftDepth = maxDepth(root->left);
	int rightDepth = maxDepth(root->right);
	return leftDepth > rightDepth ? leftDepth + 1 : rightDepth + 1;}
bool isBalanced(struct TreeNode* root)
{
	if (NULL == root)
		return true;
	int leftDepth = maxDepth(root->left);
	int rightDepth = maxDepth(root->right);
	return abs(leftDepth - rightDepth) < 2
		&& isBalanced(root->left)
		&& isBalanced(root->right);
}
//給你二叉樹的根節點 root ，返回它節點值的 前序 遍歷。
int Treesize(struct TreeNode* root)
{
	return root == NULL ? 0 : Treesize(root->left) + Treesize(root->right) + 1;
}
void PrevOrder(struct TreeNode* root, int* a, int* pi)
{
	if (NULL == root)
		return;
	a[*pi] = root->val;
	++(*pi);
	PrevOrder(root->left, a, pi);
	PrevOrder(root->right, a, pi);
}
int* preorderTraversal(struct TreeNode* root, int* returnSize) {
	int size = Treesize(root);//計算樹的節點的個數
	int* a = malloc(sizeof(int) * size);
	int i = 0;
	PrevOrder(root, a, &i);
	*returnSize = size;
	return a;
}