在算法的實現中，遍歷與遞歸是經常出現的兩種操作。遍歷其實就是使用一個for循環來遍歷集合里的元素，在編程中經常出現，通俗易懂，至于遞歸，我們先來看看遞歸的概念：在數學與計算機科學中，是指在函數的定義中使用函數自身的方法。其實遞歸在程序語言中簡單的理解就是方法自己調用自己。遞歸其實和循環是非常像的，循環都可以改寫成遞歸，遞歸未必能改寫成循環，這是一個充分不必要的條件。今天這篇文章就帶大家深入解析遞歸算法。

遞歸做為一種算法在程序設計語言中廣泛應用。一個過程或函數在其定義或說明中有直接或間接調用自身的一種方法，它通常把一個大型復雜的問題層層轉化為一個與原問題相似的規模較小的問題來求解，遞歸策略只需少量的程序就可描述出解題過程所需要的多次重復計算，大大地減少了程序的代碼量。遞歸的能力在于用有限的語句來定義對象的無限集合。一般來說，遞歸需要有邊界條件、遞歸前進段和遞歸返回段。當邊界條件不滿足時，遞歸前進；當邊界條件滿足時，遞歸返回。

構成遞歸需具備的條件：

1. 子問題須與原始問題為同樣的事，且更為簡單；

2. 不能無限制地調用本身，須有個出口，化簡為非遞歸狀況處理。

通過使用遞歸，可以把一個大型復雜的問題逐層轉化為一個與原問題相似的規模較小的問題來求解。因此如果使用遞歸，可以達到使用少量的代碼就可描述出解題過程所需的多次重復計算的目的，減少了程序的代碼量 。

下面用一個例子來具體感受一下遞歸操作：

大家應該都比較熟悉階乘的算法：3！= 3 * 2 * 1 ； 4！= 4 * 3 * 2 * 1

不難看出，在這里反復執行了一個逐漸-1和相乘的操作，如果可以使用某段代碼達到重復調用的效果就很方便了，在這里就可以使用遞歸：

func factorial(_ n:Int) -> Int{

    return n < 2 ? 1: n * factorial(n-1)

}

factorial(3) //6

在上面的代碼里，factorial函數調用了它自己，并且在n<2的時候返回了1；否則繼續調用自己。從代碼本身其實不難理解函數調用的方式，但是這個6究竟是怎么算出來的呢？這就涉及到遞歸的實現原理了。

遞歸的調用實際上是通過調用棧（callback stack）來實現的，為了加深我們的理解可結合下圖來看：

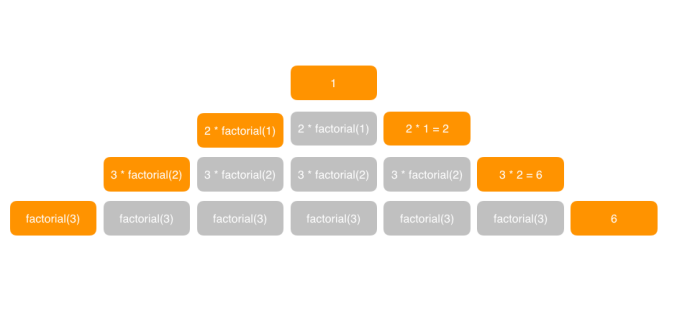
由上圖可以看出，整個遞歸的過程和棧的入棧出棧的操作非常類似：橘黃色背景的圓角矩形代表了棧頂元素，也就是正在執行的操作，而灰色背景的圓角矩形則代表了其余的元素，它們的順序就是當初被調用的順序，而且在內容上保持了當時被調用時執行的代碼。

現在我們按照時間順序從左到右來說明一下整個調用的過程：

最開始傳入3之后，3滿足了n>=2的條件，繼續調用自己：3 * factorial(2) ，入棧。

傳入2之后，2滿足了n>=2的條件，繼續調用自己：2 * factorial(1) ，入棧。

傳入1之后，1滿足了n<2的條件，停止調用自己，返回了1，出棧。

此時的棧頂元素為2 * factorial(1) ，而剛剛factorial(1)返回了1，所以現在這里變成了2 * 1 = 2，出棧。

同樣地，此時棧頂元素為3 * factorial(2)里的 factorial(2)返回了2，所以現在這里變成了3 * 2 = 6，出棧。

最后，factorial(3)返回了6，出棧，遞歸結束。

整個遞歸的過程可以大致理解為：在使遞歸繼續的條件為false之前，持續遞歸調用，以棧的形式保存調用上下文（臨時變量，函數等）。一旦這個條件變為true，則立即按照出棧的順序（入棧順序的逆序）來返回值，逐個傳遞，最終傳遞到最開始調用的那一層返回最終結果。再簡單點，遞歸中的“遞”就是入棧，傳遞調用信息；“歸”就是出棧，輸出返回值。

而這個分界線就是遞歸的終止條件。很顯然，這個終止條件在整個遞歸過程中起著舉足輕重的作用。試想一下，如果這個條件永遠不會改變，那么就會一直入棧，就會發生棧溢出的情況。事實上，遞歸算法解題相對常用的算法如普通循環等，運行效率較低。因此，在有選擇的情況下不建議使用遞歸算法。到這里關于深入解析遞歸算法的所有問題，就講完了，希望大家對于遞歸的知識有所掌握和了解，如果對遞歸相關的知識還有其它問題，我們可以在本站的數據結構和算法教程中學習更多的優秀算法，讓我們在解題有更多的選擇。