由于二叉樹是非線性結構，因此，樹的遍歷實質上是將二叉樹的各個結點轉換成為一個線性序列來表示。先序、中序、后序遍歷二叉樹的區(qū)別在于：根節(jié)點被訪問的先后。也就是每種遍歷方式的按自己獨特的規(guī)則和順序走遍二叉樹的所有結點，使每一個結點都被訪問一次，而且只被訪問一次。本文我們主要來探討一下二叉樹中序遍歷。

先訪問根節(jié)點再訪問其左右子樹，這是先序遍歷；按照左子樹、根節(jié)點、右子樹的順序訪問的方式便為中序遍歷；那么后序遍歷，自然就是先訪問左右子樹，再訪問根節(jié)點了。二叉樹的三種遍歷方式其實思想都是一樣的，掌握了一種就可以舉一反三。

中序遍歷遞歸寫法很簡單，就是直接按照定義來實現就 OK 了。

status Mid_view_root(BTpoint T,status (*view)(TElemType e)) ???//中序遍歷的遞歸寫法
{
??if(T!=NULL)
??{
????if(Mid_view_root(T->lchild,view))
??????if(Print_tree_data(T->data)) ???
????????if(Mid_view_root(T->rchild,view))
??????????return OK;
????return ERROR;
??}
??else return OK;
}

那么中序遍歷的非遞歸形式該怎么寫呢？

首先，中序遍歷（非遞歸）得用到「 棧 」這種數據結構。棧的特點是：先進后出，我們也正是利用了這個特點來實現中序遍歷的非遞歸形式。

那么，這又是如何實現的呢？

先遍歷二叉樹的根節(jié)點的左子樹到最后一個左子樹節(jié)點，按順序將它們入棧；出棧并輸出最后一個左子樹節(jié)點；讀取該節(jié)點的右子樹，重復上述操作。如果一個結點的左右子樹都被訪問過，則退回到該節(jié)點的父結點，將其輸出，讀取右子樹。如此循環(huán)，最后就能得到中序遍歷（非遞歸）的輸出了。

假設有這么一棵二叉樹：

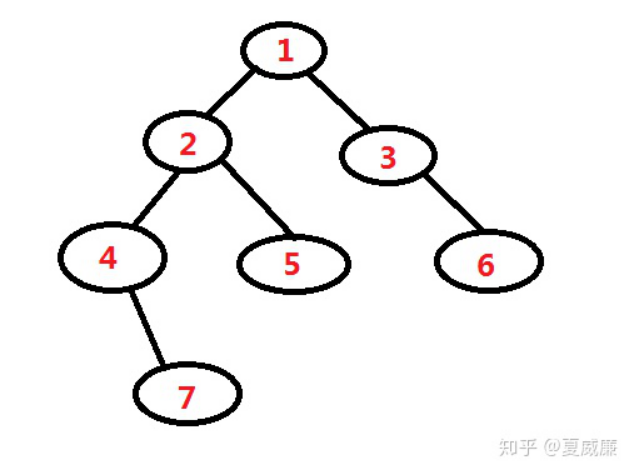
首先，結點「 1 」進棧，因為它有左子樹，讀取左子樹到最后一個左子樹結點「 4 」，在這過程中將它們按序進棧，這時棧中的元素為「1， 2， 4 」。「 4 」出棧，讀取它的右子樹，重復上述操作，得到棧中元素為「 1， 2， 7 」。「 7 」出棧，因為結點「 7 」沒有右子樹，可視為已訪問過其右子樹，退回到結點「 7 」的父結點即結點「 4 」。因為「 4 」的左右子樹都已被訪問過，退回到其父結點「 2 」，「 2 」出棧，讀取其右子樹。

代碼實現有兩種方式。一種是比較復雜的，調用了棧的幾個函數來實現該功能。

//中序遍歷二叉排序樹(非遞歸）
Status InOrderTraverse2(BiTree T)
{
????SqStack S;
????BiTree p;
????p=(BiTree)malloc(sizeof(BiTNode));
????InitStack(S); ?// 構建一個空棧
???p=T;
????while(p||!StackEmpty(S)) ??// StackEmpty( S ) ?判斷棧是否為空
???{
????????if(p)
????????{
????????????Push(S,p); ???????// 入棧
???????????p=p->lchild;
????????}
????????else
????????{
????????????Pop(S,p); ??????// 出棧
???????????if(!PrintElement(p->data)) ????// 輸出結點的值
???????????????return ERROR;
????????????p=p->rchild;
????????}
????}
????printf("\n");
????return OK;
}

第二種就很簡潔了，不需要那么多個函數，幾乎與我們的思路一模一樣：

//中序遍歷序列(非遞歸算法)
status M_nonrecursive(BTpoint T,Stack S) ???????
{
??while(T!=NULL||S.base!=S.top)
??{
????while(T!=NULL)
????{
??????*S.top++=T;
??????T=T->lchild;
????}
????T=*--S.top;
????Print_tree_data(T->data); ??// 輸出結點的值
???T=T->rchild;
??}
??return OK;
}

至于二叉樹前序和后序遍歷，基本上很容易就能推導出來了，因為二者遍歷方式和二叉樹中序遍歷有許多的共通之處，在本站的數據結構和算法教程中，對二叉樹遍歷所有方式有一個完整的描述和整理，感興趣的小伙伴可以前去觀看，收集這些優(yōu)秀的資料，化為己用，我們也能夠實現知識積累的跨越。