一、遞歸概念

    遞歸本質(zhì)：程序調(diào)用自身的編程技巧叫做遞歸。

    程序調(diào)用自身的編程技巧稱為遞歸（recursion）。遞歸做為一種算法在程序設(shè)計語言中廣泛應(yīng)用。一個過程或函數(shù)在其定義或說明中有直接或間接調(diào)；

    用自身的一種方法，它通常把一個大型復(fù)雜的問題層層轉(zhuǎn)化為一個與原問題相似的規(guī)模較小的問題來求解，遞歸策略只需少量的程序就可描述出解題過；

    程所需要的多次重復(fù)計算，大大地減少了程序的代碼量。遞歸的能力在于用有限的語句來定義對象的無限集合。

    （一）遞歸的三個條件：

    邊界條件

    遞歸前進(jìn)段

    遞歸返回段

    當(dāng)邊界條件不滿足時，遞歸前進(jìn)；當(dāng)邊界條件滿足時，遞歸返回。

    下面通過兩個示例程序來說明：

    使用Java代碼求5的階乘。（5的階乘=5*4*3*2*1）

    此題中，按照遞歸的三個條件來分析：

    (1)邊界條件：階乘，乘到最后一個數(shù)，即1的時候，返回1，程序執(zhí)行到底；

    (2)遞歸前進(jìn)段：當(dāng)前的參數(shù)不等于1的時候，繼續(xù)調(diào)用自身；

    (3)遞歸返回段：從最大的數(shù)開始乘，如果當(dāng)前參數(shù)是5，那么就是5*4，即5*(5-1)，即n*(n-1)

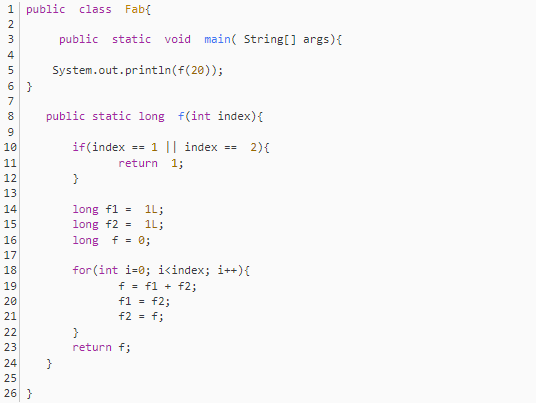
    使用Java代碼求數(shù)列：1，1，2，3，5，8......第40位的數(shù)

    此題的突破口在：從第3位數(shù)開始，本位數(shù)是前兩位數(shù)的和。要計算第多少位的值，那么就需要將位數(shù)作為參數(shù)傳進(jìn)方法進(jìn)行計算。

    (1)首先，當(dāng)位數(shù)為1和2時，當(dāng)前返回的值應(yīng)該是1；

    (2)然后，當(dāng)位數(shù)為3時，返回值應(yīng)該=2=1+1；

    當(dāng)位數(shù)為4時，返回值=3=2+1；

    當(dāng)位數(shù)為5時，返回值=5=3+2；

    當(dāng)位數(shù)為6時，返回值=8=5+3；

    ......

    (3)由(2)得知，大于等于3的情況下，當(dāng)前位數(shù)（n）的數(shù)值=f(n-1)+f(n-2)

    （二）非遞歸方法實現(xiàn)（迭代方法）

    迭代本質(zhì)：利用變量的原值推算出變量的一個新值，迭代就是A不停的調(diào)用B.

    通過觀察推導(dǎo)，找到解決問題的方法，發(fā)現(xiàn)其中的規(guī)律，將其轉(zhuǎn)化成程序語言表達(dá)出來。

    本質(zhì)：使用合適的數(shù)據(jù)類型變量代替問題中的數(shù)據(jù)，將解決問題的方法轉(zhuǎn)化為符合程序語言的邏輯。

    遞歸其實是方便了程序員難為了機(jī)器，遞歸可以通過數(shù)學(xué)公式很方便的轉(zhuǎn)換為程序。其優(yōu)點就是易理解，容易編程。但遞歸是用棧機(jī)制實現(xiàn)的，每深入一層，都要占去一塊棧數(shù)據(jù)區(qū)域，對嵌套層數(shù)深的一些算法，遞歸會力不從心，空間上會以內(nèi)存崩潰而告終，而且遞歸也帶來了大量的函數(shù)調(diào)用，這也有許多額外的時間開銷。所以在深度大時，它的時空性就不好了。（會占用大量的內(nèi)存空間）

    而迭代雖然效率高，運行時間只因循環(huán)次數(shù)增加而增加，沒什么額外開銷，空間上也沒有什么增加，但缺點就是不容易理解，編寫復(fù)雜問題時困難。

    能不用遞歸就不用遞歸，遞歸都可以用迭代來代替。（要辯證的看待這個問題，深度不大，還是可以采用遞歸的）。

　以上就是動力節(jié)點java培訓(xùn)機(jī)構(gòu)的小編針對“Java基礎(chǔ)學(xué)習(xí)：java方法遞歸調(diào)用”的內(nèi)容進(jìn)行的回答，希望對大家有所幫助，如有疑問，請在線咨詢，有專業(yè)老師隨時為你服務(wù)。