更新時間:2022-12-01 10:37:13 來源:動力節點 瀏覽1254次
先序遍歷:先序遍歷結果為3 4 6 5 8 9,就拿樹的左枝為例,3是根,打印,4是3的左孩子,打印,6是4的左孩子,打印,6的左孩子為空,所以返回到4,然后去找4的右孩子,4的右孩子也為空,返回到3,這就是左子樹遍歷的過程。然后非遞歸主要用到棧來存儲結點,棧先進后出,所以應該是右孩子先入棧,左孩子后入棧,這樣pop就能先得到左孩子。先將根結點3入棧,接下來就是開始循環,循環結束的條件就是棧為空,先彈出棧頂,再打印棧頂,如果棧頂的右孩子不為null,就把右孩子放進棧中,如果棧頂的左孩子不為null,就把左孩子放入棧中。
void pretravel2(TreeNode root) {
if (root == null) return;
Stack<TreeNode> s = new Stack<TreeNode>();
s.push(root);
while (!s.isEmpty()) {
TreeNode node = s.pop();
System.out.print(node.val+" ");
if (node.right != null) {
s.push(node.right);
}
if (node.left != null) {
s.push(node.left);
}
}
}
中序遍歷:中序遍歷的結果為6 4 3 8 5 9,其實就是左遍歷完了,彈出根,找根的右結點,整個過程是先一路找左結點,找到左結點為null的6,然后找6的根4,接著找4的右,為null,接著找4的根3,接著一路找3的左,直到結點的左孩子為null,這就找到了8,然后找8的根5,再找5的右9,這樣就找完了。他們的入棧出棧順序:根結點入棧,左孩子直接入棧,并且標記這個結點已經走過,以防后面再走,當發現哪個結點的左孩子為null的時候,就打印這個結點,并且將這個結點出棧,讓他的右孩子入棧。
void intravel2(TreeNode root) {
if(root==null)
return ;
Stack<TreeNode> stack=new Stack<>();
stack.push(root);
//使用list來標記結點是否走過
List<TreeNode> list=new ArrayList<>();
while(!stack.isEmpty()) {
//只需要拿到根結點,不需要pop出來
TreeNode peek = stack.peek();
//如果左孩子不為null并且左孩子沒有被走過,就把他放到棧里,并且標記為走過
if(peek.left!=null&& !list.contains(peek.left)) {
stack.push(peek.left);
list.add(peek.left);
}
else {//左孩子為空,打印根結點,根結點出棧,右孩子進棧
TreeNode pop = stack.pop();
System.out.print(pop.val+" ");
if(pop.right!=null)
stack.push(pop.right);
}
}
}
中序遍歷還有另外一種寫法:
void intravel3(TreeNode root) {
Stack<TreeNode> stack=new Stack<>();
TreeNode p=root;
while(p!=null||!stack.isEmpty()) {
while(p!=null) {
stack.push(p);
p=p.left;
}
//左孩子遍歷完了,根結點彈出,打印根結點,遍歷右孩子
if(!stack.isEmpty()) {
TreeNode temp=stack.pop();
System.out.print(temp.val+" ");
p=temp.right;
}
}
}
后序遍歷: 后序遍歷的結果為6 4 8 9 5 3,一路找左結點到6,然后找到右孩子為null,退到根4,4的右為null,然后3的左孩子遍歷完了,到右孩子,一路找左孩子到8,右孩子9,根5,右孩子遍歷完,最后到4。他們的進棧出棧順序為:根結點入棧,左孩子一路入棧,當有個結點的左孩子為null的時候,就將它的右孩子入棧,如果右孩子也為null,才打印根結點。
void postrval2(TreeNode root) {
if(root==null)
return ;
Stack<TreeNode> stack=new Stack<>();
stack.push(root);
List<TreeNode> list=new ArrayList<>();
while(!stack.isEmpty()) {
TreeNode peek=stack.peek();
//先一路走左,左走完了才到右
if(peek.left!=null&&!list.contains(peek.left)) {
//如果左結點不為null并且左結點沒有走過
//就將其壓入棧中,并且標記已經走過
stack.push(peek.left);
list.add(peek.left);
}
else {
if(peek.right!=null&&!list.contains(peek.right)) {
//如果右結點為不為null并且右結點沒有走過
//就將右結點壓入棧中,標記已經走過
stack.push(peek.right);
list.add(peek.right);
}
else {
//如果右孩子為null,就打印根結點
TreeNode pop = stack.pop();
System.out.print(pop.val+" ");
}
}
}
}
遞歸遍歷,非遞歸遍歷的代碼
import java.util.ArrayList;
import java.util.List;
import java.util.Scanner;
import java.util.*;
class TreeNode {
int val;
TreeNode left=null;
TreeNode right=null;
TreeNode(){}
TreeNode(int val) {
this.val=val;
}
}
public class Main {
public static void main(String[] args) {
Main main = new Main();
TreeNode root=null;
root=main.createTree();
System.out.println("先序遍歷:");
main.pretravel(root);
System.out.println("");
System.out.println("中序遍歷:");
main.intravel(root);
System.out.println("");
System.out.println("后序遍歷:");
main.postravel(root);
System.out.println("");
System.out.println("迭代先序遍歷:");
main.pretravel2(root);
System.out.println("");
System.out.println("迭代中序遍歷1(類似于回溯算法):");
main.intravel2(root);
System.out.println("");
System.out.println("迭代中序遍歷2:");
main.intravel3(root);
System.out.println("");
System.out.println("迭代后序遍歷:");
main.postrval2(root);
System.out.println("");
System.out.println("層序遍歷:");
main.levelOrder(root);
}
//建樹
TreeNode createTree(){
Scanner sc=new Scanner(System.in);
int temp=sc.nextInt();
if(temp<=0)return null;
TreeNode root=new TreeNode();
root.val=temp;
root.left=createTree();
root.right=createTree();
return root;
}
//先序
void pretravel(TreeNode root){
if(root==null)return;
System.out.print(root.val+" ");
pretravel(root.left);
pretravel(root.right);
}
//中序
void intravel(TreeNode root){
if(root==null)return;
intravel(root.left);
System.out.print(root.val+" ");
intravel(root.right);
}
//后序
void postravel(TreeNode root){
if(root==null)return;
postravel(root.left);
postravel(root.right);
System.out.print(root.val+" ");
}
//迭代先序
void pretravel2(TreeNode root) {
if (root == null) return;
Stack<TreeNode> s = new Stack<TreeNode>();
s.push(root);
while (!s.isEmpty()) {
TreeNode node = s.pop();
System.out.print(node.val+" ");
if (node.right != null) {
s.push(node.right);
}
if (node.left != null) {
s.push(node.left);
}
}
}
void intravel2(TreeNode root) {
if(root==null)
return ;
Stack<TreeNode> stack=new Stack<>();
stack.push(root);
List<TreeNode> list=new ArrayList<>();
while(!stack.isEmpty()) {
TreeNode peek = stack.peek();
if(peek.left!=null&& !list.contains(peek.left)) {
stack.push(peek.left);
list.add(peek.left);
}
else {//左孩子為空,打印根結點,根結點出棧,右孩子進棧
TreeNode pop = stack.pop();
System.out.print(pop.val+" ");
if(pop.right!=null)
stack.push(pop.right);
}
}
}
void intravel3(TreeNode root) {
Stack<TreeNode> stack=new Stack<>();
TreeNode p=root;
while(p!=null||!stack.isEmpty()) {
while(p!=null) {
stack.push(p);
p=p.left;
}
if(!stack.isEmpty()) {
TreeNode temp=stack.pop();
System.out.print(temp.val+" ");
p=temp.right;
}
}
}
void postrval2(TreeNode root) {
if(root==null)
return ;
Stack<TreeNode> stack=new Stack<>();
stack.push(root);
List<TreeNode> list=new ArrayList<>();
while(!stack.isEmpty()) {
TreeNode peek=stack.peek();
if(peek.left!=null&&!list.contains(peek.left)) {
stack.push(peek.left);
list.add(peek.left);
}
else {
if(peek.right!=null&&!list.contains(peek.right)) {
stack.push(peek.right);
list.add(peek.right);
}
else {
TreeNode pop = stack.pop();
System.out.print(pop.val+" ");
}
}
}
}
//層序
void levelOrder(TreeNode root) {
List<TreeNode> list=new ArrayList<>();
list.add(root);
while(list.size()!=0) {
TreeNode temp=list.get(0);
if(temp.left!=null) list.add(temp.left);
if(temp.right!=null) list.add(temp.right);
list.remove(0);
System.out.print(temp.val+" ");
}
}
}
輸入是按照先序序列輸,輸一個打一個回車,結點為null的時候輸入-1,表示為空,葉子節點要輸兩個-1,表示左右孩子均為空。
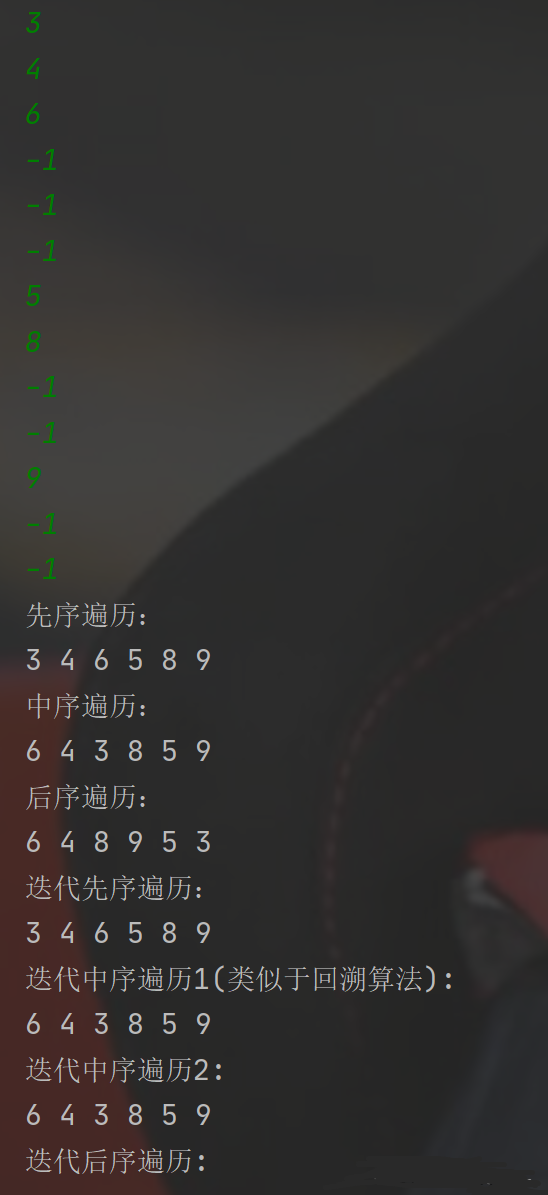

以上就是關于“非遞歸遍歷二叉樹的3種方法”的介紹,本站的數據結構和算法教程對二叉樹遍歷方式有非常詳細的講解,不需要我們過多的推導,但我們學習的時候應該更注重理解,這樣才能夠學有所思。
 Java實驗班
Java實驗班
0基礎 0學費 15天面授
 Java就業班
Java就業班
有基礎 直達就業
 Java夜校直播班
Java夜校直播班
業余時間 高薪轉行
 Java在職加薪班
Java在職加薪班
工作1~3年,加薪神器
 Java架構師班
Java架構師班
工作3~5年,晉升架構
提交申請后,顧問老師會電話與您溝通安排學習

