Java多線程和并發面試題（附答案）第6題

6、ConcurrentSkipListMap非阻塞Hash跳表集合？

大家都是知道TreeMap，它是使用樹形結構的方式進行存儲數據的線程不安全的Map集合（有序的哈希表），并且可以對Map中的Key進行排序，Key中存儲的數據需要實現Comparator接口或使用CompareAble接口的子類來實現排序。

ConcurrentSkipListMap也是和TreeMap，它們都是有序的哈希表。但是，它們是有區別的：

● 第一，它們的線程安全機制不同，TreeMap是非線程安全的，而ConcurrentSkipListMap是線程安全的。

● 第二，ConcurrentSkipListMap是通過跳表實現的，而TreeMap是通過紅黑樹實現的。

● 那現在我們需要知道什么是跳表？

Skip list(跳表）是一種可以代替平衡樹的數據結構，默認是按照Key值升序的。Skip list讓已排序的數據分布在多層鏈表中，以0-1隨機數決定一個數據的向上攀升與否，通過“空間來換取時間”的一個算法，在每個節點中增加了向前的指針，在插入、刪除、查找時可以忽略一些不可能涉及到的結點，從而提高了效率。

從概率上保持數據結構的平衡比顯式的保持數據結構平衡要簡單的多。對于大多數應用，用Skip list要比用樹算法相對簡單。由于Skip list比較簡單，實現起來會比較容易，雖然和平衡樹有著相同的時間復雜度O(log(n))，但是Skip list的常數項會相對小很多。Skip list在空間上也比較節省。一個節點平均只需要1.333個指針（甚至更少）。下圖為Skip list結構圖

（以7，14，21，32，37，71，85序列為例）。

● SkipList性質

● 由很多層結構組成，level是通過一定的概率隨機產生的。

● 每一層都是一個有序的鏈表，默認是升序，也可以根據創建映射時所提供的Comparator進行排序，具體取決于使用的構造方法。

● 最底層（Level 1）的鏈表包含所有元素。

● 如果一個元素出現在Level i的鏈表中，則它在Level i之下的鏈表也都會出現。

● 每個節點包含兩個指針，一個指向同一鏈表中的下一個元素，一個指向下面一層的元素。

● 什么是ConcurrentSkipListMap？

ConcurrentSkipListMap提供了一種線程安全的并發訪問的排序映射表。內部是SkipList（跳表）結構實現，在理論上能夠在O(log(n))時間內完成查找、插入、刪除操作。

注意：調用ConcurrentSkipListMap的size時，由于多個線程可以同時對映射表進行操作，所以映射表需要遍歷整個鏈表才能返回元素個數，這個操作是個O(log(n))的操作。

● ConcurrentSkipListMap 的數據結構，如下圖所示：

說明：可以看到ConcurrentSkipListMap的數據結構使用的是跳表，每一個HeadIndex、Index結點都會包含一個對Node的引用，同一垂直方向上的Index、HeadIndex結點都包含了最底層的Node結點的引用。并且層級越高，該層級的結點（HeadIndex和Index）數越少。Node結點之間使用單鏈表結構。

● ConcurrentSkipListMap源碼分析

ConcurrentSkipListMap主要用到了Node和Index兩種節點的存儲方式，通過volatile關鍵字實現了并發的操作

static final class Node<K, V> {
    final K key;
    volatile Object value;//value 值
    volatile Node<K, V> next;//next 引用
……
}

static class Index<K, V> {
    final Node<K, V> node;
    final Index<K, V> down;//downy 引用
    volatile Index<K, V> right;//右邊引用
……
}

● ConcurrentSkipListMap查找操作

通過SkipList的方式進行查找操作：（下圖以“查找91”進行說明：）

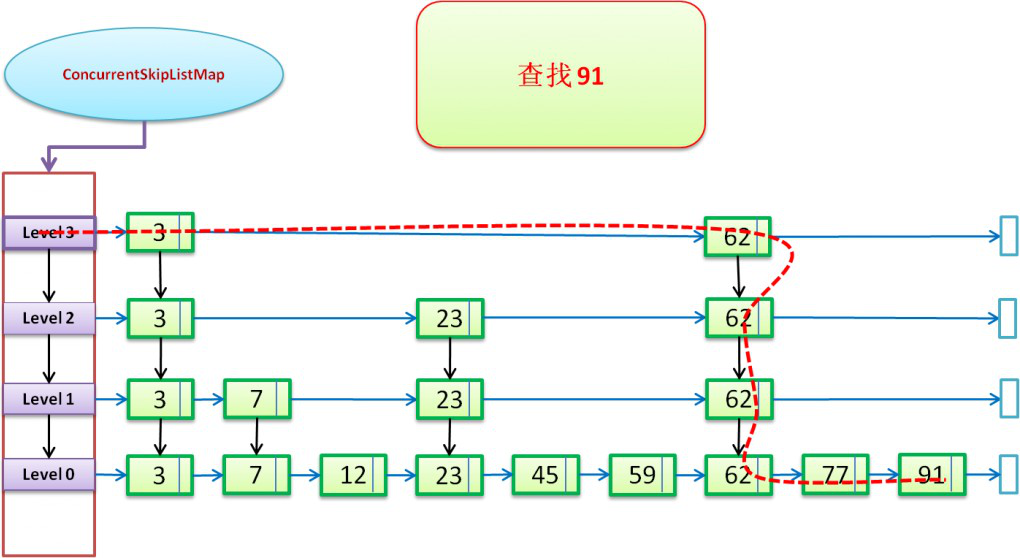
紅色虛線，表示查找的路徑，藍色向右箭頭表示right引用；黑色向下箭頭表示down引用；下面就是源碼中的實現（get方法是通過doGet方法來時實現的）。

private V doGet(Object okey) {
    Comparable<? super K> key = comparable(okey);
    for (; ; ) {
        // 找到“key對應的節點”
        Node<K, V> n = findNode(key);
        if (n == null)
            return null;
        Object v = n.value;
        if (v != null)
            return (V) v;
    }
}

● ConcurrentSkipListMap刪除操作

通過SkipList的方式進行刪除操作：（下圖以“刪除23”進行說明：）。

紅色虛線，表示查找的路徑，藍色向右箭頭表示right引用；黑色向下箭頭表示down引用；下面就是源碼中的實現（remove方法是通過doRemove方法來時實現的）。

//remove 操作,通過 doRemove 實現,把所有 level 中出現關鍵字 key 的地方都 delete 掉
public V remove(Object key) {
    return doRemove(key, null);
}

final V doRemove(Object okey, Object value) {
    Comparable<? super K> key = comparable(okey);
    for (; ; ) {
        Node<K, V> b = findPredecessor(key);//得到 key 的前驅（就是比 key 小的最大節點）
        Node<K, V> n = b.next;//前驅節點的 next 引用
        for (; ; ) {//遍歷
            if (n == null)//如果 next 引用為空,直接返回
                return null;
            Node<K, V> f = n.next;
            if (n != b.next)    // 如果兩次獲得的 b.next 不是相同的 Node,就跳轉到第一層循環重新獲得 b 和 n
                break;
            Object v = n.value;
            if (v == null) {    // 當 n 被其他線程 delete 的時候,其 value==null, 此時做輔助處理,并重新獲取 b 和 n
                n.helpDelete(b, f);
                break;
            }
            if (v == n || b.value == null)    // 當其前驅被 delet 的時候直接跳出,重新獲取 b 和 n break;
                int c = key.compareTo(n.key);
            if (c < 0)
                return null;
            if (c > 0) {//當 key 較大時就繼續遍歷
                b = n;
                n = f;
                continue;
            }
            if (value != null && !value.equals(v)) return null;
            if (!n.casValue(v, null)) break;
            if (!n.appendMarker(f) || !b.casNext(n, f))//casNext 方法就是通過比較和設置 b（前驅）的 next 節點的方式來實現刪除操作
                findNode(key);    // 通過嘗試 findNode 的方式繼續 find
            else {
                findPredecessor(key);    // Clean index
                if (head.right == null)    //如果 head 的 right 引用為空,則表示不存在該 level
                    tryReduceLevel();
            }
            return (V) v;
        }
    }
}

● ConcurrentSkipListMap插入操作

通過SkipList的方式進行插入操作：（下圖以“添加55”的兩種情況，進行說明：）。

 

在level=2（該level存在）的情況下添加55的圖示:只需在level<=2的合適位置插入55即可在level=4(該level不存在，圖示level4是新建的)的情況下添加55的情況：首先新建level4，然后在level<=4的合適位置插入55。

下面就是源碼中的實現（put方法是通過doPut方法來時實現的）。

/put 操作,通過 doPut 實現
    public V put(K key, V value) {
        if (value == null)
            throw new NullPointerException();
        return doPut(key, value, false);
    }

    private V doPut(K kkey, V value, boolean onlyIfAbsent) {
        Comparable<? super K> key = comparable(kkey);
        for (; ; ) {
            Node<K, V> b = findPredecessor(key);//前驅
            Node<K, V> n = b.next;
            //定位的過程就是和 get 操作相似
            for (; ; ) {
                if (n != null) {
                    Node<K, V> f = n.next;
                    if (n != b.next) // 前后值不一致的情況下,跳轉到第一層循環重新獲得 b 和 n
                        break;
                    Object v = n.value;
                    if (v == null) {    // n 被 delete 的情況下
                        n.helpDelete(b, f);
                        break;
                    }
                    if (v == n || b.value == null) // b 被 delete 的情況,重新獲取 b 和 n
                        break;
                    int c = key.compareTo(n.key);
                    if (c > 0) {
                        b = n;
                        n = f;
                        continue;
                    }
                    if (c == 0) {
                        if (onlyIfAbsent || n.casValue(v, value)) return (V) v;
                        else
                            break; // restart if lost race to replace value
                    }
                    // else c < 0; fall through
                }
                Node<K, V> z = new Node<K, V>(kkey, value, n);
                if (!b.casNext(n, z))
                    break;    // restart if lost race to append to b
                int level = randomLevel();//得到一個隨機的 level 作為該 key-value 插入的最高 level
                if (level > 0)
                    insertIndex(z, level);//進行插入操作
                return null;
            }
        }
    }

    /**
     * 獲得一個隨機的 level 值
     */
    private int randomLevel() {

        int x = randomSeed;
        x ^= x << 13;
        x ^= x >>> 17;
        randomSeed = x ^= x << 5;
        if ((x & 0x8001) != 0) // test highest and lowest bits
            return 0;
        int level = 1;
        while (((x >>>= 1) & 1) != 0) ++level;
        return level;
    }

    //執行插入操作：如上圖所示,有兩種可能的情況：
//1.當 level 存在時,對 level<=n 都執行 insert 操作
//2.當 level 不存在（大于目前的最大 level）時,首先添加新的 level,然后在執行操作 1
    private void insertIndex(Node<K, V> z, int level) {
        HeadIndex<K, V> h = head;
        int max = h.level;
        if (level <= max) {//情況 1
            Index<K, V> idx = null;
            for (int i = 1; i <= level; ++i)//首先得到一個包含 1~level 個級別的 down 關系的鏈表, 最后的 inx 為最高 level
                idx = new Index<K, V>(z, idx, null);
            addIndex(idx, h, level);//把最高 level 的 idx 傳給 addIndex 方法
        } else { // 情況 2 增加一個新的級別
            level = max + 1;
            Index<K, V>[] idxs = (Index<K, V>[]) new Index[level + 1];
            Index<K, V> idx = null;
            for (int i = 1; i <= level; ++i)//該步驟和情況 1 類似
                idxs[i] = idx = new Index<K, V>(z, idx, null);
            HeadIndex<K, V> oldh;
            int k;
            for (; ; ) {
                oldh = head;
                int oldLevel = oldh.level;
                if (level <= oldLevel) { // lost race to add level
                    k = level;
                    break;
                }
                HeadIndex<K, V> newh = oldh;
                Node<K, V> oldbase = oldh.node;
                for (int j = oldLevel + 1; j <= level; ++j)
                    newh = new HeadIndex<K, V>(oldbase, newh, idxs[j], j);//創建新的
                if (casHead(oldh, newh)) {
                    k = oldLevel;
                    break;
                }
            }
            addIndex(idxs[k], oldh, k);
        }

    }

    /**
     * 在 1~indexlevel 層中插入數據
     */
    private void addIndex(Index<K, V> idx, HeadIndex<K, V> h, int indexLevel) {
        // insertionLevel 代表要插入的 level,該值會在 indexLevel~1 間遍歷一遍
        int insertionLevel = indexLevel;
        Comparable<? super K> key = comparable(idx.node.key);
        if (key == null) throw new NullPointerException();
        // 和 get 操作類似,不同的就是查找的同時在各個 level 上加入了對應的 key
        for (; ; ) {
            int j = h.level;
            Index<K, V> q = h;
            Index<K, V> r = q.right;
            Index<K, V> t = idx;
            for (; ; ) {
                if (r != null) {
                    Node<K, V> n = r.node;
                    // compare before deletion check avoids needing recheck
                    int c = key.compareTo(n.key);
                    if (n.value == null) {
                        if (!q.unlink(r))
                            break;
                        r = q.right;
                        continue;
                    }
                    if (c > 0) {
                        q = r;
                        r = r.right;
                        continue;
                    }
                }
                if (j == insertionLevel) {//在該層 level 中執行插入操作
                    // Don't insert index if node already deleted
                    if (t.indexesDeletedNode()) {
                        findNode(key); // cleans up
                        return;
                    }
                    if (!q.link(r, t))//執行 link 操作,其實就是 inset 的實現部分
                        break; // restart
                    if (--insertionLevel == 0) {
                        // need final deletion check before return
                        if (t.indexesDeletedNode())
                            findNode(key);
                        return;
                    }
                }
                if (--j >= insertionLevel && j < indexLevel)//key 移動到下一層 level
                    t = t.down;
                q = q.down;
                r = q.right;
            }
        }
    }