- Java教程
- Java語言概述
- Java語言發(fā)展史
- Java語言的特性
- Java中JDK、JRE、JVM三者之間的關(guān)系
- Java程序的開發(fā)過程與運(yùn)行過程
- 編寫第一個(gè)Java程序
- Java中的注釋
- Java中public class與class的區(qū)別
- Java運(yùn)算符概述
- Java算術(shù)運(yùn)算符
- Java關(guān)系運(yùn)算符
- Java邏輯運(yùn)算符
- Java位運(yùn)算符
- Java賦值運(yùn)算符
- Java條件運(yùn)算符
- Java字符串連接運(yùn)算符
- Java控制語句概述
- Java選擇語句if
- Java switch選擇語句
- Java for循環(huán)語句
- Java while循環(huán)語句
- Java do while循環(huán)語句
- Java break語句
- Java continue語句
- Java return語句
- Java方法的作用及本質(zhì)
- Java方法的定義及調(diào)用
- Java方法返回值詳解
- Java棧數(shù)據(jù)結(jié)構(gòu)
- Java方法執(zhí)行過程中內(nèi)存的變化
- Java遞歸方法
- Java方法重載
- Java對象的創(chuàng)建和使用方法
- Java虛擬機(jī)內(nèi)存管理
- Java構(gòu)造方法Constructor
- Java空指針異常
- Java實(shí)例變量是一個(gè)引用
- Java方法調(diào)用時(shí)參數(shù)的傳遞問題
- Java中this關(guān)鍵字是什么
- Java this關(guān)鍵字的使用(在實(shí)例方法中)
- Java this關(guān)鍵字的使用(在構(gòu)造方法中)
- Java中static關(guān)鍵字
- Java中static靜態(tài)變量
- Java static靜態(tài)代碼塊
- Java static靜態(tài)方法
Java遞歸方法
什么是方法遞歸?我們先來看一段代碼:
public class RecursionTest01 {
public static void main(String[] args) {
m();
}
public static void m(){
System.out.println("m begin");
m();
System.out.println("m over");
}
}
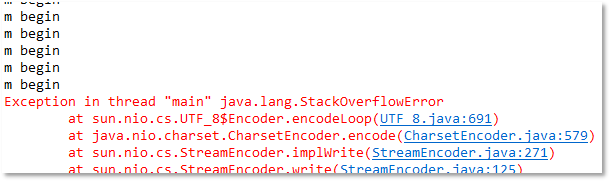
以上代碼的執(zhí)行結(jié)果如下圖所示:
圖7-17:遞歸執(zhí)行結(jié)果
我們可以看到以上代碼的執(zhí)行過程中,一直輸出“m begin”,“m over”一次也沒有輸出,直到最終發(fā)生了錯(cuò)誤:java.lang.StackOverflowError,這個(gè)錯(cuò)誤是棧內(nèi)存溢出錯(cuò)誤,錯(cuò)誤發(fā)生后,JVM退出了,程序結(jié)束了。
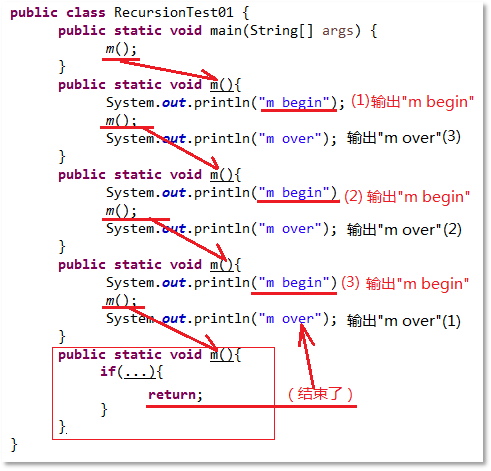
實(shí)際上以上代碼在m()方法執(zhí)行過程中又調(diào)用了m()方法,方法自身調(diào)用自身,這就是方法遞歸調(diào)用。以上程序?qū)嶋H上等同于以下的偽代碼(說明問題,但是無法執(zhí)行的代碼):
圖7-18:說明遞歸執(zhí)行原理的偽代碼
通過偽代碼我們可以看出,m()方法一直在被調(diào)用(方法中的代碼必須遵循自上而下的順序依次逐行執(zhí)行,不能跳行執(zhí)行),對于棧內(nèi)存來說一直在進(jìn)行壓棧操作,m()方法從未結(jié)束過,所以沒有彈棧操作,即使棧內(nèi)存足夠大(也是有限的內(nèi)存),總有一天棧內(nèi)存會(huì)不夠用的,這個(gè)時(shí)候就會(huì)出現(xiàn)棧內(nèi)存溢出錯(cuò)誤。通過以上研究得出遞歸必須要有合法的結(jié)束條件,沒有結(jié)束條件就一定會(huì)發(fā)生StackOverflowError。我們再來看看有結(jié)束條件的遞歸,例如以下代碼:
圖7-19:遞歸的過程中滿足了某個(gè)條件,遞歸結(jié)束了
綜上所述,遞歸其實(shí)就是方法在執(zhí)行的過程中調(diào)用了另一個(gè)方法,而另一個(gè)方法則是自己本身。在代碼角度來看就是在a()方法中調(diào)用a()方法,使用遞歸須謹(jǐn)慎,因?yàn)檫f歸在使用的時(shí)候必須有結(jié)束條件,沒有結(jié)束條件就會(huì)導(dǎo)致無終止的壓棧,棧內(nèi)存最終必然會(huì)溢出,程序因錯(cuò)誤的發(fā)生而終止。
大家再來思考一個(gè)問題,一個(gè)遞歸程序有合法有效的結(jié)束條件就一定不會(huì)發(fā)生棧內(nèi)存溢出錯(cuò)誤嗎?在實(shí)際開發(fā)中遇到這個(gè)錯(cuò)誤應(yīng)該怎么辦?
一個(gè)遞歸程序有的時(shí)候存在合法有效的終止條件,但由于遞歸的太深,在還沒有等到條件成立的時(shí)候,棧內(nèi)存已經(jīng)發(fā)生了溢出,這種情況也是存在的,所以實(shí)際開發(fā)中我們盡可能使用循環(huán)來代替遞歸算法,原則是:能不用遞歸盡量不用,能用循環(huán)代替的盡可能使用循環(huán)。當(dāng)然,如果在開發(fā)中遇到了由于使用遞歸導(dǎo)致棧內(nèi)存溢出錯(cuò)誤的發(fā)生,首先,我們要檢查遞歸的終止條件是否合法,如果是合法的還是發(fā)生棧內(nèi)存溢出錯(cuò)誤,那么我們可以嘗試調(diào)整堆棧空間的大小。怎么調(diào)整堆棧大小呢,大家可以研究一下下圖中的一些參數(shù),這里就不再講解內(nèi)存大小的調(diào)整了,這不是初級程序員應(yīng)該掌握的。
圖7-20:java虛擬機(jī)內(nèi)存設(shè)置參數(shù)
接下來我們來研究一下在不使用遞歸的前提下,完成1~N的求和,這個(gè)應(yīng)該很簡單,請看下面代碼:
public class RecursionTest02 {
public static void main(String[] args) {
int n = 5;
int result = accumulate(n);
System.out.println("1到" + n + "的和是:" + result);
}
public static int accumulate(int n){
int result = 0;
for(int i = 1;i <= n; i++){
result += i;
}
return result;
}
}
運(yùn)行結(jié)果如下圖所示:

圖7-21:不使用遞歸計(jì)算1~N的和
那么,使用遞歸應(yīng)該怎么寫呢?請看以下代碼:
public class RecursionTest03 {
public static void main(String[] args) {
int n = 5;
int result = accumulate(n);
System.out.println("1到" + n + "的和是:" + result);
}
public static int accumulate(int n){
if(n == 1){
return 1;
}
return n + accumulate(n - 1);
}
}
運(yùn)行結(jié)果如下圖所示:

圖7-22:使用遞歸計(jì)算1~N的和
我們來使用偽代碼對以上代碼的執(zhí)行過程進(jìn)行分析,請看以下偽代碼:
public static int accumulate(int n){ //假設(shè)n是5
if(n == 1){
return 1;
}
return n + accumulate(n - 1);
//return 5 + accumulate(4); return 5 + 4 + 3 + 2 + 1;
}
public static int accumulate(int n){
if(n == 1){
return 1;
}
return n + accumulate(n - 1);
//return 4 + accumulate(3); return 4 + 3 + 2 + 1;
}
public static int accumulate(int n){
if(n == 1){
return 1;
}
return n + accumulate(n - 1);
//return 3 + accumulate(2); return 3 + 2 + 1;
}
public static int accumulate(int n){
if(n == 1){
return 1;
}
return n + accumulate(n - 1);
//return 2 + accumulate(1); return 2 + 1;
}
public static int accumulate(int n){
if(n == 1){
return 1; //這行代碼執(zhí)行了 return 1;
}
}
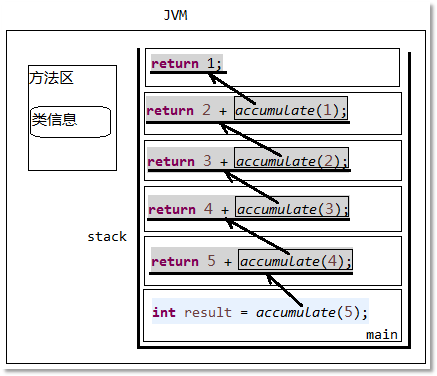
以上程序的內(nèi)存變化是這樣的,請看下圖:
圖7-23:1~N遞歸求和內(nèi)存圖
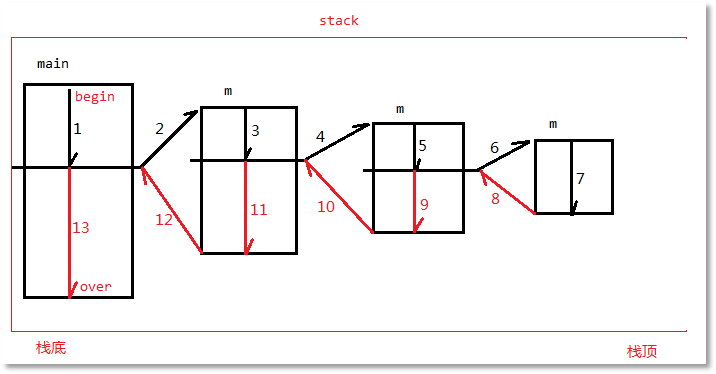
為了加強(qiáng)大家對遞歸算法的理解,我們再來看一張圖:
圖7-24:另一種形式的遞歸內(nèi)存圖
其實(shí)大家把上圖逆時(shí)針旋轉(zhuǎn)90度,你會(huì)看到一個(gè)棧數(shù)據(jù)結(jié)構(gòu)對嗎?