![]() 二叉樹面試題
二叉樹面試題
暴力遞歸是把問題轉化為規模縮小的同類問題的子問題 ,有明確的不需要繼續進行遞歸的條件(base case),有當得到了子問題的結果之后的決策過程并且不記錄每一個子問題的解。
相傳在古印度圣廟中,有一種被稱為漢諾塔(Hanoi)的游戲。該游戲是在一塊銅板裝置上,有三根桿(編號A、B、C),在A桿自下而上、由大到小按順序放置64個金盤。
游戲的目標:把A桿上的金盤全部移到C桿上,并仍保持原有順序疊好。
操作規則:每次只能移動一個盤子,并且在移動過程中三根桿上都始終保持大盤在下,小盤在上,操作過程中盤子可以置于A、B、C任一桿上。
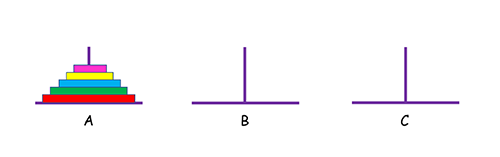
思想
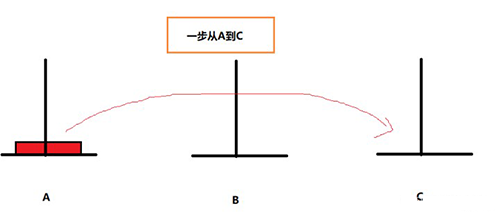
假設只有一個盤子
如果有兩個盤子
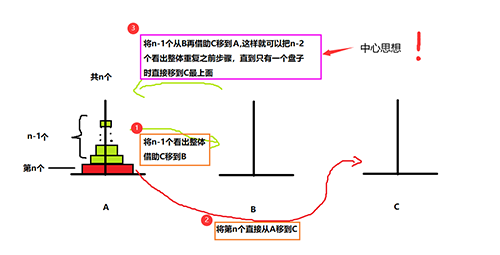
// 1~i 圓盤 目標是from -> to, other是另外一個
public static void func(int N, String from, String to, String other) {
if (N == 1) { // base
System.out.println("Move 1 from " + from + " to " + to);
} else {
func(N - 1, from, other, to);
System.out.println("Move " + N + " from " + from + " to " + to);
func(N - 1, other, to, from);
}
}
打印一個字符串的全部子序列,包括空字符串
有字符串“abc”,字符串長度為3,下標分別是0,1,2。則決策的過程一共有三個,令初始序列為空字符串。分別是:
0:此時有兩種情況,要不要'a',如果要,子序列變為“a”;如果不要則還是空字符串;
1:此時有兩種情況,要不要‘b’,加上上一步的兩種這里就有4種情況,這里不一一列舉;
2:此時有兩種情況,要不要‘c’,加上上一步的四種情況這里就有8種情況。
public class PrintAllSubsquences {
public static void pringAllSub(char[] str, int i, String res) {
if (i == str.length) {
System.out.println(res);
return;
}
//兩種情況
pringAllSub(str, i + 1, res);
pringAllSub(str, i + 1, res + str[i]);
}
public static void main(String[] args) {
String str = "abc";
pringAllSub(str.toCharArray(), 0, "");
}
}
n 皇后問題研究的是如何將 n 個皇后放置在 n×n 的棋盤上,并且使皇后彼此之間不能相互攻擊(同一行、同一列、同一斜線上的皇后都會自動攻擊)。
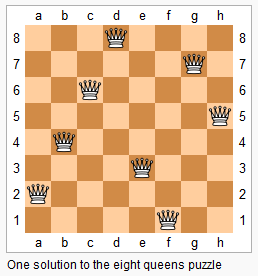
思路
1. 準備一個數組record[i],record[i] 表示 i行的皇后,放在了第幾列
2. 如果第一個皇后的在i1行j1列,第二個皇后在i1行j2列,那么應該滿足的條件是
不能共斜線:|i1-i2|不等于|j1-j2|
不能共行: i1不等于i2
不能共列:j1不等于j2
public class NQueens {
public static int num1(int n) {
if (n < 1) {
return 0;
}
int[] record = new int[n]; // record[i] -> i行的皇后,放在了第幾列
return process1(0, record, n);
}
// 返回值是,擺完所有的皇后,合理的擺法有多少種
public static int process1(int i, int[] record, int n) {
if (i == n) { // 終止行
return 1;
}
int res = 0;
for (int j = 0; j < n; j++) { // 當前行在i行,嘗試i行所有的列 -> j
// 當前i行的皇后,放在j列,會不會和之前(0..i-1)的皇后,不共行共列或者共斜線,
// 如果是,認為有效
// 如果不是,認為無效
if (isValid(record, i, j)) {
record[i] = j;
res += process1(i + 1, record, n);
}
}
return res;
}
// 返回i行皇后,放在了j列,是否有效
public static boolean isValid(int[] record, int i, int j) {
for (int k = 0; k < i; k++) { // 之前的某個k行的皇后
if ((j == record[k]) ||(Math.abs(record[k] - j) == Math.abs(i - k))) {
return false;
}
}
return true;
}
}
小明走樓梯,一次可以跨兩個臺階,也可以跨一個臺階,求有n個臺階,一共有多少種跨發?
從問題中我們可以分析出,如果邁上最后一個臺階,可以是一步,也可以是兩步。
分析:
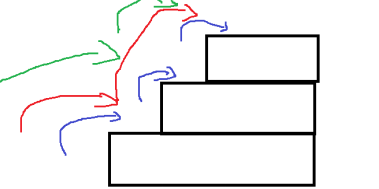
可以理解為:
f(n)=f(n-1)+f(n-2)
同理:
f(n-1)=f(n-1-1)+f(n-1-2)
f(n-2)=f(n-2-1)+f(n-2-2)
. …
…
f(4)=f(3)+f(2)
f(3)=f(2)+f(1)
f(2)=2
f(1)=1
int getNum(int n) {
if (n <= 0)return 0;
if (n == 1) return 1;
if (n == 2) return 2;
int arr = new int[n+1];
arr[1] = 1;
arr[2] = 2;
for (int i = 3; i <= n; i++) {
arr[i] = arr[i - 1] + arr[i - 2];
}
int ret = arr[n];
return ret;
}