001什么是堆排序？

堆結(jié)構(gòu)如下圖，堆的實(shí)際結(jié)構(gòu)是數(shù)組，但是我們?cè)诜治鏊臅r(shí)候用的是有特殊標(biāo)準(zhǔn)的完全二叉樹(shù)來(lái)分析。也就是說(shuō)數(shù)組是堆的實(shí)際物理結(jié)構(gòu)而完全二叉樹(shù)是我們便于分析的邏輯結(jié)構(gòu)。堆有兩種：大根堆和小根堆。每個(gè)節(jié)點(diǎn)的值都大于其左孩子和右孩子節(jié)點(diǎn)的值，稱為大根堆。每個(gè)節(jié)點(diǎn)的值都小于其左孩子和右孩子節(jié)點(diǎn)的值，稱為小根堆。

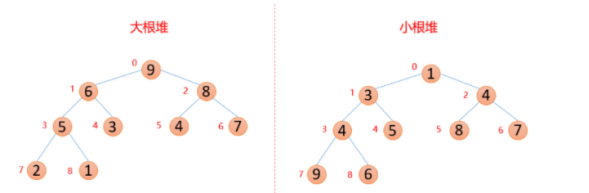
上面的結(jié)構(gòu)映射成數(shù)組就變成了下面這個(gè)樣子

002堆排序的特點(diǎn)？

1.首先堆的大小是提前知道的，根節(jié)點(diǎn)的位置上存儲(chǔ)的數(shù)據(jù)總是在數(shù)組的第一個(gè)元素。

2.假設(shè)一個(gè)非根節(jié)點(diǎn)所存儲(chǔ)的數(shù)據(jù)的索引為i，那么它的父節(jié)點(diǎn)存儲(chǔ)的數(shù)據(jù)所對(duì)應(yīng)的索引就為[(i-1)/2]

3.假設(shè)一個(gè)節(jié)點(diǎn)所存儲(chǔ)的數(shù)據(jù)的索引為i，那么它的孩子（如果有）所存儲(chǔ)的數(shù)據(jù)分別所對(duì)應(yīng)的索引為：左孩子是[2*i+1]，右孩子是[2*i+2]

003堆排序的流程？

第一步，將待排序的數(shù)組構(gòu)造成一個(gè)大根堆，假設(shè)有下面這個(gè)數(shù)組：

具體思路：第一次保證0~0位置大根堆結(jié)構(gòu)，第二次保證0~1位置大根堆結(jié)構(gòu)，第三次保證0~2位置大根堆結(jié)構(gòu)...直到保證0~n-1位置大根堆結(jié)構(gòu)（每次新插入的數(shù)據(jù)都與其父節(jié)點(diǎn)進(jìn)行比較，如果插入的數(shù)比父節(jié)點(diǎn)大，則與父節(jié)點(diǎn)交換。周而復(fù)始一直向上比較，直到小于等于父節(jié)點(diǎn)或者來(lái)到了根節(jié)點(diǎn)則終止）

【1】插入6的時(shí)候，6大于他的父節(jié)點(diǎn)3，即arr(1)>arr(0)，則交換；此時(shí)保證了0~1位置是大根堆結(jié)構(gòu)，如下圖：

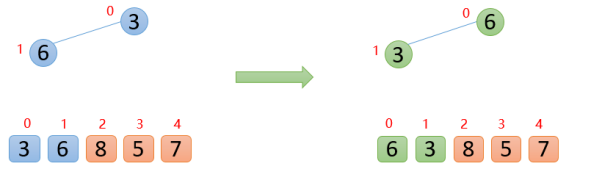
【2】插入8的時(shí)候，8大于其父節(jié)點(diǎn)6，即arr(2)>arr(0),則交換；此時(shí)，保證了0~2位置是大根堆結(jié)構(gòu)，如下圖

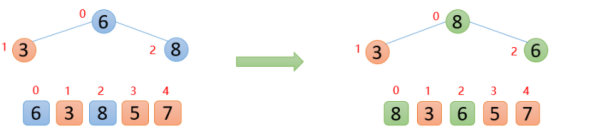
【3】插入5的時(shí)候，5大于其父節(jié)點(diǎn)3，則交換，交換之后，5又發(fā)現(xiàn)比8小，所以不交換；此時(shí)，保證了0~3位置大根堆結(jié)構(gòu)，如下圖

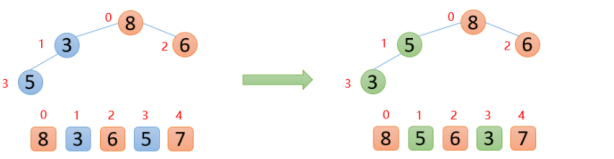
【4】插入7的時(shí)候，7大于其父節(jié)點(diǎn)5，則交換，交換之后，7又發(fā)現(xiàn)比8小，所以不交換；此時(shí)整個(gè)數(shù)組已經(jīng)是大根堆結(jié)構(gòu)

第二步，將根節(jié)點(diǎn)的數(shù)與末尾的數(shù)交換

【1】大根堆中整個(gè)數(shù)組的最大值就是堆結(jié)構(gòu)的父節(jié)點(diǎn)，接下來(lái)將根節(jié)點(diǎn)的數(shù)8與末尾的數(shù)5交換

第三步，將剩余的n-1個(gè)數(shù)再構(gòu)造成大根堆

如上圖所示，此時(shí)最大數(shù)8已經(jīng)來(lái)到末尾，讓堆的有效大小減1，后面拿頂端的數(shù)與其左右孩子較大的數(shù)進(jìn)行比較，如果頂端的數(shù)大于其左右孩子較大的數(shù)，則停止，如果頂端的數(shù)小于其左右孩子較大的數(shù)，則交換；周而復(fù)始一直向下比較，直到大于左右孩子較大的數(shù)或者沒(méi)有孩子節(jié)點(diǎn)則終止。

下圖中，5的左右孩子中，左孩子7比右孩子6大，則5與7進(jìn)行比較，發(fā)現(xiàn)5<7，則交換；交換后，發(fā)現(xiàn)5已經(jīng)大于他的左孩子，說(shuō)明剩余的數(shù)已經(jīng)構(gòu)成大根堆，

第四步，再將第二步和第三步反復(fù)執(zhí)行，便能得到有序數(shù)組

004如何將待排序的數(shù)組構(gòu)造成一個(gè)大根堆？

首先遍歷該數(shù)組，假設(shè)某個(gè)數(shù)處于index位置，每次都讓index位置和父節(jié)點(diǎn)位置的數(shù)進(jìn)行比較，如果大于父節(jié)點(diǎn)的值就交換位置，....周而復(fù)始，一直到不能往上為止。

for (int i = 0; i < arr.length; i++) { // O(N)
    while (arr[index] > arr[(index - 1) / 2]) {
        swap(arr, index, (index - 1) / 2);
        index = (index - 1) / 2;
    }	
}

005如何將剩余的n-1個(gè)數(shù)再構(gòu)造成大根堆？

先將大根堆的頭節(jié)點(diǎn)的數(shù)據(jù)與堆上的最后一個(gè)數(shù)交換位置后，把堆有效區(qū)的長(zhǎng)度減1，再?gòu)念^節(jié)點(diǎn)開(kāi)始做向下的比較，每次都和左右孩子中較大值進(jìn)行比較，如果父節(jié)點(diǎn)比最大孩子的值下就交換位置....周而復(fù)始，一直到不能往下為止。

// 某個(gè)數(shù)在index位置，能否往下移動(dòng)
public static void heapify(int[] arr, int index, int heapSize) {
    int left = index * 2 + 1; // 左孩子的下標(biāo)
    while (left < heapSize) { // 下方還有孩子的時(shí)候
        // 兩個(gè)孩子中，誰(shuí)的值大，把下標(biāo)給largest		
        int largest = left + 1 < heapSize && arr[left + 1] > arr[left] ? left + 1 : left;
        // 父和較大的孩子之間，誰(shuí)的值大，把下標(biāo)給largest
        largest = arr[largest] > arr[index] ? largest : index;
        if (largest == index) {
            break;	
        }
        swap(arr, largest, index);
        index = largest;
        left = index * 2 + 1;
    }
}

006堆的排序如何實(shí)現(xiàn)？

具體實(shí)現(xiàn)前面的問(wèn)題，具體源代碼實(shí)現(xiàn)如下：

public static void heapSort(int[] arr) {
    if (arr == null || arr.length < 2) {
        return;
    }
    //第一步，將待排序的數(shù)組構(gòu)造成一個(gè)大根堆
    for (int i = 0; i < arr.length; i++) { // O(N)
        heapInsert(arr, i); // O(logN)
    }
    int heapSize = arr.length;
    //第二步，將根節(jié)點(diǎn)的數(shù)與末尾的數(shù)交換
    swap(arr, 0, --heapSize);
    while (heapSize > 0) { // O(N)
        //第三步，將剩余的n-1個(gè)數(shù)再構(gòu)造成大根堆
        heapify(arr, 0, heapSize); // O(logN)
        //第二步，將根節(jié)點(diǎn)的數(shù)與末尾的數(shù)交換
        swap(arr, 0, --heapSize); // O(1)
    }
}

007什么是桶排序？

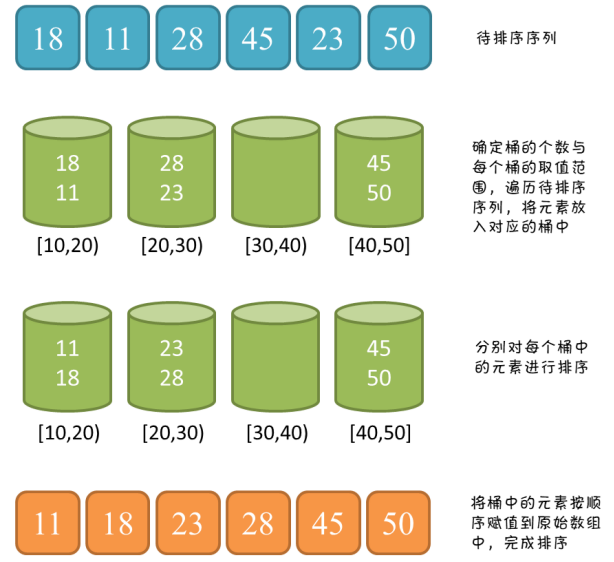
1）桶排序（Bucket sort）或所謂的箱排序，是一個(gè)排序算法，工作的原理是將數(shù)組分到有限數(shù)量的桶里。每個(gè)桶再個(gè)別排序（有可能再使用別的排序算法或是以遞歸方式繼續(xù)使用桶排序進(jìn)行排序），最后依次把各個(gè)桶中的記錄列出來(lái)記得到有序序列。桶排序是鴿巢排序的一種歸納結(jié)果。當(dāng)要被排序的數(shù)組內(nèi)的數(shù)值是均勻分配的時(shí)候，桶排序使用線性時(shí)間（Θ(n)）。但桶排序并不是比較排序，他不受到O(n log n)下限的影響。

2）算法圖解

008堆排序平均執(zhí)行的時(shí)間復(fù)雜度和需要附加的存儲(chǔ)空間復(fù)雜度分別是( )

A. O(n^2)和O(1)
B. O(nlog(n))和O(1)
C. O(nlog(n))和O(n)
D. O(n^2)和O(n)
答案：B
解析：暫無(wú)解析