001樹的相關術語。

樹：樹是由根節點和若干顆子樹構成的。樹是由一個集合以及在該集合上定義的一種關系構成的。集合中的元素稱為樹的節點，所定義的關系稱為父子關系。
二叉樹：樹是由根節點和若干子樹構成的。每個節點最多含有兩個子樹的樹稱為二叉樹。
度：一個結點含有的子樹的個數
葉子節點或終端節點：度為0的節點
節點的層數： 樹根到節點的路徑長度是該節點的層數，節點都有層數，根所在的層為0
樹的高度或深度：樹的高度或深度是樹中節點的最大層數（最長路徑的長度）加1 ，空樹高度為0，只有根節點的樹高度為1。  

002二叉樹有哪幾種遍歷方式。

(1)先序遍歷:先訪問根節點，然后訪問左子樹，若當前節點無左子樹，則訪問當前節點的右子樹；
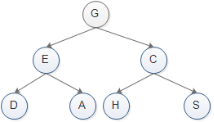
如上圖：
1.訪問該二叉樹的根節點，找到 G；
2.訪問節點 G 的左子樹，找到節點 E；
3.訪問節點 E的左子樹，找到節點 D；
4.由于訪問節點 D左子樹失敗，且也沒有右子樹，因此以節點 D為根節點的子樹遍歷完成。 但節點 E 還沒有遍歷其右子樹，因此現在開始遍歷，即訪問節點 A；
5.由于節點 A 無左右子樹，因此節點 A 遍歷完成，并且由此以節點 E 為根節點的子樹也遍歷完成。現在回到節點 G ，并開始遍歷該節點的右子樹，即訪問節點 C；
6.訪問節點 C 左子樹，找到節點 H；
7.由于節點 H無左右子樹，因此節點 H 遍歷完成，回到節點 C 并遍歷其右子樹，找到節點 S；
8.節點 S 無左右子樹，因此以節點 S為根節點的子樹遍歷完成，同時回歸節點 G。由于節點 G 的左右子樹全部遍歷完成，因此整個二叉樹遍歷完成；
9.最終遍歷的結果就是：GEDACHS
(2)中序遍歷:先訪問左子樹，然后訪問根節點，最后訪問右子樹，即左根右。所以遍歷的結果是：DEAGHCS。
(3)后序遍歷:先訪問左孩子，然后訪問右孩子，最后訪問根節點，即左右根。所以遍歷的結果是：DAEHSCG。
(4)寬度遍歷:從根節點開始依次遍歷左子節點和右子節點，直到所有子節點都變遍歷完為止。所以遍歷的結果是：GECDAHS。

003二叉樹的遍歷有什么規律？

1.前序遍歷的第一個遍歷節點必是根節點，而后序遍歷的最后一個遍歷節點必是根節點；
2.根據中序遍歷順序無法判斷根節點，但若已知根節點，則可根據中序遍歷順序判斷出左子樹的組成元素和右子樹的組成元素；

004二叉樹遍歷的遞歸實現。

算法思路：
1.首先通過先序遍歷【GEDACHS】或者后序遍歷【DAEHSCG】可以得到二叉樹的根節點G，通過中序遍歷【DEAGHCS】可以得到左右子樹的成員，即左子樹的成員【DEA】,右子樹的成員是【HCS】。
2.然后將左子樹【DEA】看作新的二叉樹，通過后序遍歷【DAEHSCG】可以得到新二叉樹的根節點為E。又通過中序遍歷【DEAGHCS】可以得到A為E的右子樹，D為E的左子樹。
3.右子樹HCS同理
依此類推，即可畫出整棵二叉樹。不難看出，畫出這棵二叉樹的順序，就是我們想要得到的先序輸出順序，因此我們只需要在畫二叉樹時，對當前根節點進行輸出，即可完成題目需要。這樣只需要設置節點輸出的位置就可以得到對應的遍歷結果。

public class Node {
    public int data;
	public Node leftChild;
	public Node rightChild;

	public Node(int data) {
		this.data = data;
	}
}
public static void OrderTraveral(TreeNode node){
    if(node == null){
        return;
    }
    //遞歸前序遍歷   根-> 左-> 右
    /*
    System.out.print(node.data+" ");
    OrderTraveral(node.leftChild);
    OrderTraveral(node.rightChild);*/
    
    //遞歸中序遍歷   左-> 根-> 右
    /*
    OrderTraveral(node.leftChild);
    System.out.print(node.data+" ");
    OrderTraveral(node.rightChild);*/
    
    //遞歸后序遍歷   左-> 右->根
    /*
    OrderTraveral(node.leftChild);
    OrderTraveral(node.rightChild);
    System.out.print(node.data+" ");*/
}

005非遞歸實現二叉樹的先序遍歷。

先序的思路：采用棧的先進后出思想進行實現的
1.首先有一個棧s1。
2.先將頭結點入棧s1。
3.頭結點出棧，判斷當前結點的右孩子是不是為空，不為空則入棧；判斷當前結點的左孩子是不是為空不為空則入棧。周而復始依次迭代。

public static void preOrder(Node head) {
	System.out.print("pre-order: ");
	if (head != null) {
		Stack<Node> stack = new Stack<Node>();
		stack.add(head);
		while (!stack.isEmpty()) {
			head = stack.pop();
			System.out.print(head.value + " ");
			if (head.right != null) {
				stack.push(head.right);
			}
			if (head.left != null) {
				stack.push(head.left);
			}
		}
	}
	System.out.println();
}

006非遞歸實現二叉樹的中序遍歷。

中序的思路：采用棧的先進后出思想進行實現的
1.首先有一個棧s1。
2.判斷頭結點是不是為空，不為空則入棧s1，并獲取頭結點的左節點。如果為空則出棧頭結點，并獲取頭結點的右節點。周而復始依次迭代。

public static void inOrder(Node head) {
	System.out.print("in-order: ");
	if (head != null) {
		Stack<Node> stack = new Stack<Node>();
		while (!stack.isEmpty() || head != null) {
			if (head != null) {
				stack.push(head);
				head = head.left;
			} else {
				head = stack.pop();
				System.out.print(head.value + " ");
				head = head.right;
			}
		}
	}
	System.out.println();
}

007非遞歸實現二叉樹的后序遍歷。

后序思路：
1.首先有兩個棧s1和s2
2.先講頭結點入棧s1
3.棧s1的頭結點出棧并入棧s2,判斷當前結點的左孩子是不是為空，不為空則入棧s1；判斷當前結點的右孩子是不是為空不為空則入棧s1。周而復始依次迭代，這樣循環完后s2棧的入棧的順序就是頭右左；
4.將s2彈棧，周而復始依次迭代，彈出的順序為左右頭；

public static void posOrder(Node head) {
	System.out.print("pos-order: ");
	if (head != null) {
		Stack<Node> s1 = new Stack<Node>();
		Stack<Node> s2 = new Stack<Node>();
		s1.push(head);
		while (!s1.isEmpty()) {
			head = s1.pop();
			s2.push(head);
			if (head.left != null) {
				s1.push(head.left);
			}
			if (head.right != null) {
				s1.push(head.right);
			}
		}
		while (!s2.isEmpty()) {
			System.out.print(s2.pop().value + " ");
		}
	}
	System.out.println();
}

008非遞歸實現二叉樹的寬度遍歷。

寬度遍歷思路：
1.首先有一個隊列queue1和一個levelMap
2.先講頭結點入隊queue1
3.隊列queue1的頭結點出隊并輸出當前節點，判斷當前結點的左孩子是不是為空，不為空則入隊queue1；判斷當前結點的右孩子是不是為空不為空則入隊queue1。周而復始依次迭代；

public static void width(Node head) {
	if(head == null) {
		return 0;
	}
	Queue<Node> queue = new LinkedList<>();
	queue.add(head);
	while(!queue.isEmpty()) {
		Node cur = queue.poll();
        System.out.println(cur.value);
		if(cur.left!=null) {
			queue.add(cur.left);
		} 
        if(cur.right!=null) {
			queue.add(cur.right);
		} 
	}
}