001什么是基數(shù)排序？

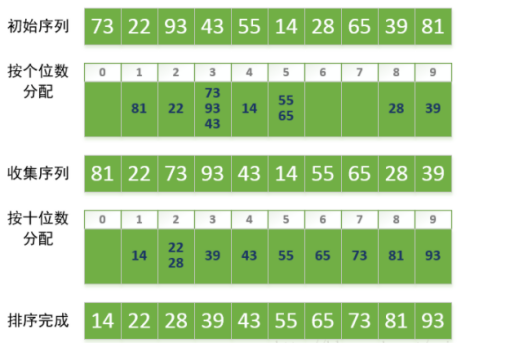
1）基數(shù)排序是對(duì)桶排序的一種改進(jìn)，這種改進(jìn)是讓“桶排序”適合于更大的元素值集合的情況，而不是提高性能。它的基本思想是：將整數(shù)按位數(shù)切割成不同的數(shù)字，然后按每個(gè)位數(shù)分別比較。

2）算法圖解

第一步，將所有待比較數(shù)值根據(jù)個(gè)位數(shù)的數(shù)值分別分配至編號(hào)0到9的桶中；

第二步，桶中數(shù)據(jù)根據(jù)先進(jìn)先出的原則出來，收集完整的序列；

第三步，十位、百位....周而復(fù)始

002基數(shù)排序的代碼實(shí)現(xiàn)？

//digit代表最大的數(shù)有幾個(gè)十進(jìn)制位
public static void radixSort(int[] arr, int L, int R, int digit) {
    //十進(jìn)制數(shù)
    final int radix = 10;
    int i = 0, j = 0;
    // 有多少個(gè)數(shù)準(zhǔn)備多少個(gè)輔助空間
    int[] bucket = new int[R - L + 1];
    for (int d = 1; d <= digit; d++) { // 有多少位就循環(huán)幾次
        //十進(jìn)制的數(shù)，創(chuàng)建長(zhǎng)度為10的數(shù)組
        int[] count = new int[radix]; // count[0..9]
        for (i = L; i <= R; i++) {
            j = getDigit(arr[i], d);//獲取該數(shù)的個(gè)位、十位、百位......上的數(shù)
            count[j]++;//獲取數(shù)組中每個(gè)數(shù)每位分別是1、2、3....9數(shù)分別總共有幾個(gè)
        }
        for (i = 1; i < radix; i++) {
            //獲取數(shù)組中每個(gè)數(shù)每位分別是<=1、<=2、<=3....<=9數(shù)分別總共有幾個(gè)
            count[i] = count[i] + count[i - 1];
        }
        for (i = R; i >= L; i--) {
            j = getDigit(arr[i], d);//獲取該數(shù)的個(gè)位、十位、百位......上的數(shù)
            bucket[count[j] - 1] = arr[i];//將數(shù)放回到輔助空間
            count[j]--;
        }
        for (i = L, j = 0; i <= R; i++, j++) {
            arr[i] = bucket[j];
        }
    }
}
//獲取該數(shù)的個(gè)位、十位、百位......上的數(shù)	
public static int getDigit(int x, int d) {		
    return ((x / ((int) Math.pow(10, d - 1))) % 10);
}