![]() 二叉樹面試題
二叉樹面試題
1)歸并排序采用了分治策略(divide-and-conquer),就是將原問題分解為一些規模較小的相似子問題,然后遞歸解決這些子問題,最后合并其結果作為原問題的解。
2)算法圖解
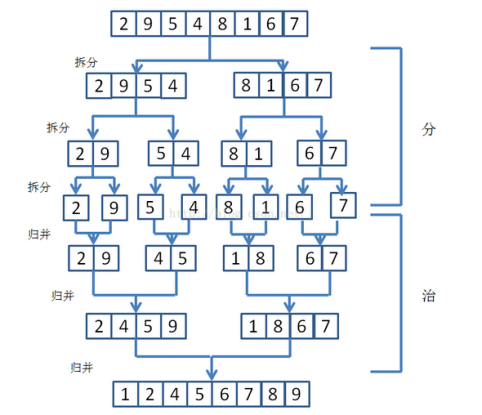
【1】如圖:先將數組分兩半,左邊是【2、9、5、4】,右邊是【8、1、6、7】;
【2】將左邊【2、9、5、4】繼續分兩半,左邊是【2、9】,右邊是【5、4】;
【3】將【2、9】繼續分兩半,左邊是【2】,右邊是【9】;將【5、4】繼續分兩半,左邊是【5】,右邊是【4】;
【5】創建臨時輔助數組,將左邊【2】和右邊【9】通過比較大小進行合并【2、9】;
【6】創建臨時輔助數組,將左邊【5】和右邊【4】通過比較大小進行合并【4、5】;
【7】創建臨時輔助數組,將左邊【2、9】和右邊【4、5】通過比較大小進行合并【2、4、5、9】,同樣的道理得到【1、8、6、7】;
【8】創建臨時輔助數組,將左邊【2、4、5、9】和右邊【1、8、6、7】通過比較大小進行合并【1、2、4、5、6、7、8、9】;
public static void mergeSort(int[] arr) {
if (arr == null || arr.length < 2) {
return;
}
process(arr, 0, arr.length - 1);
}
public static void process(int[] arr, int L, int R) {
if (L == R) {
return;
}
int mid = L + ((R - L) >> 1);
process(arr, L, mid);
process(arr, mid + 1, R);
merge(arr, L, mid, R);
}
public static void merge(int[] arr, int L, int M, int R) {
int[] help = new int[R - L + 1];
int i = 0;
int p1 = L;
int p2 = M + 1;
while (p1 <= M && p2 <= R) {
help[i++] = arr[p1] <= arr[p2] ? arr[p1++] : arr[p2++];
}
while (p1 <= M) {
help[i++] = arr[p1++];
}
while (p2 <= R) {
help[i++] = arr[p2++];
}
for (i = 0; i < help.length; i++) {
arr[L + i] = help[i];
}
}
A. 歸并排序使用了分治策略的思想
B. 歸并排序使用了貪心策略的思想
C. 子序列的長度一定相等
D. 歸并排序是穩定的
答案:AD
解析:暫無解析
A. 6
B. 3
C. 5
D. 4
答案:C
解析:每次將工作區裝滿,共計3110400/400=7776個歸并段,對于n路歸并排序,m個歸并段,需要歸并排序的次數為次,代入數據得到答案為5,所以C正確。