![]() 二叉樹面試題
二叉樹面試題
鏈表是一種動態的數據結構,因為在創建鏈表時,我們不需要知道鏈表的長度,當插入一個結點時,只需要為該結點分配內存,然后調整指針的指向來確保新結點被連接到鏈表中。所以,它不像數組,內存是一次性分配完畢的,而是每添加一個結點分配一次內存。正是因為這點,所以它沒有閑置的內存,比起數組,空間效率更高。
1)單向鏈表,雙向鏈表
單向:每個節點只有一個后繼指針next指向后面的節點,結尾通常指向null
雙向:包含兩個指針,prev指向前一節點,next指向后一節點
2)帶頭鏈表,不帶頭鏈表
3)循環的,非循環的
循環:特殊的單鏈表,尾結點指向頭節點
首先創建節點類:單鏈表中的節點應該具有兩個屬性:val 和 next。val存儲的該節點的數據值,next存儲下一個節點的地址。下面提供兩種創建鏈表的方式:分別是枚舉法和尾插法。
class ListNode {
int val;
ListNode next;
public ListNode(int val) {
this.val = val;
}
}
枚舉法:直接進行val的賦值以及對next的初始化。
public ListNode head;//鏈表的頭
public void creatList(){
ListNode listNode1 = new ListNode(11);
ListNode listNode2 = new ListNode(22);
ListNode listNode3 = new ListNode(33);
ListNode listNode4 = new ListNode(44);
this.head=listNode1;
listNode1.next = listNode2;
listNode2.next = listNode3;
listNode3.next = listNode4;
}
class ListNode {
int val;
ListNode next;
public ListNode(int val) {
this.val = val;
}
}
尾插法:插入第一個節點時,直接將該節點賦值給head,之后每次插入新節點都會通過head.next移動到最后一個節點cur,然后將新節點賦值給cur.next。
public ListNode head;//鏈表的頭
public void add(int data){
ListNode node = new ListNode(data);
if(this.head == null){
this.head = node;
}else {
ListNode cur = this.head;
while(cur.next != null){
cur = cur.next;
}
cur.next = node;
}
}
頭結點head是不動的,通過head.next不斷移動,在移動的過程中輸出鏈表的內容。
public void display(){
ListNode cur = this.head;
while(cur != null){
System.out.print(cur.val+" ");
cur = cur.next;
}
System.out.println();
}
思路:根據棧先進后出的特點,在遍歷鏈表時,把值按順序放入棧中,最后出棧就是逆序了。
/**
* 棧
*/
public List<Integer> printListFromQueue(ListNode listNode) {
Stack<Integer> stack = new Stack<>();
while (listNode != null) {
stack.add(listNode.value);
listNode = listNode.next;
}
List<Integer> list = new ArrayList<>();
while (!stack.isEmpty()) {
list.add(stack.pop());
}
return list;
}
思路:因為遞歸的本質也是用的棧,所以先遞歸輸出它的后面節點,再輸出自己,這樣鏈表就反過來了。
/**
* 遞歸
*/
public List<Integer> printListFromDG(ListNode listNode) {
List<Integer> list = new ArrayList<>();
if (listNode != null) {
list.addAll(printListFromDG(listNode.next));
list.add(listNode.value);
}
return list;
}
將鏈表元素都賦值到數組中,然后可以從數組兩端向中間對比。
將鏈表元素全部壓棧,然后一邊出棧,一邊重新遍歷鏈表,一邊比較,只要有一個不相等,那就不是回文鏈表了。
public boolean isPalindrome(ListNode head) {
ListNode temp = head;
Stack<Integer> stack = new Stack();
//把鏈表節點的值存放到棧中
while (temp != null) {
stack.push(temp.val);
temp = temp.next;
}
//然后再出棧
while (head != null) {
if (head.val != stack.pop()) {
return false;
}
head = head.next;
}
return true;
}
上面方法的改造,先遍歷第一遍,得到總長度。之后一遍歷鏈表,一遍壓棧。當到達鏈表長度一半的位置之后,就不再壓棧,而是一邊出棧,一遍遍歷,一遍比較,只要有一個不相等,就不是回文鏈表。
public boolean isPalindrome(ListNode head) {
if (head == null)
return true;
ListNode temp = head;
Stack<Integer> stack = new Stack();
//鏈表的長度
int len = 0;
//把鏈表節點的值存放到棧中
while (temp != null) {
stack.push(temp.val);
temp = temp.next;
len++;
}
//len長度除以2
len >>= 1;
//然后再出棧
while (len-- >= 0) {
if (head.val != stack.pop())
return false;
head = head.next;
}
return true;
}
我們使用快慢指針 ,fast一次走兩步,slow一次走一步。當fast到達表尾的時候,slow正好到達一半的位置,那么接下來可以從頭開始逆序一半的元素,或者從slow開始逆序一半的元素,都可以。
public boolean isPalindrome(ListNode head) {
if(head == null || head.next == null) {
return true;
}
ListNode slow = head, fast = head;
ListNode pre = head, prepre = null;
while(fast != null && fast.next != null) {
pre = slow;
slow = slow.next;
fast = fast.next.next;
//將前半部分鏈表反轉
pre.next = prepre;
prepre = pre;
}
if(fast != null) {
slow = slow.next;
}
while(pre != null && slow != null) {
if(pre.val != slow.val) {
return false;
}
pre = pre.next;
slow = slow.next;
}
return true;
}
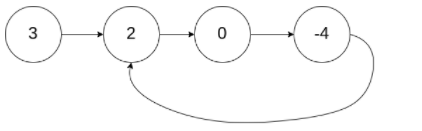
思路:循環鏈表將鏈表節點(注意是節點,不是節點里的值)存入到hashset中,如果元素添加不進去則證明有環。
public static boolean hasCycle1(ListNode head){
//存入的是ListNode類型而不是值
HashSet<ListNode> hashSet = new HashSet<>();
while (head!=null){
if (!hashSet.add(head)){
return true;
}
head=head.next;
}
return false;
}
復雜度分析:
時間復雜度:O(N),其中 N 是鏈表中的節點數。最壞情況下我們需要遍歷每個節點一次。
空間復雜度:O(N),其中 N 是鏈表中的節點數。主要為哈希表的開銷,最壞情況下我們需要將每個節點插入到哈希表中一次。
解決思路:定義兩個指針,一個指針每次移動一個位置為慢指針,一個指針每次移動兩個位置為快指針。當兩個指針相遇時就證明有環,如果快指針或者慢指針下一個節點為null,則證明無環。
為什么兩個指針一定會相遇呢?
兩個指針一旦進入環,遍歷的時候相當于無限循環因為出不出來環啊。想象一下時鐘,時針分針秒針在不同速度遍歷時是不是會相遇呢?
public static boolean hasCycle2(ListNode head){
if (head==null || head.next==null){
return false;
}
//定義兩個指針,快指針比慢指針多一步
ListNode slow = head;
ListNode fast = head.next;
while (slow!=fast){
if (fast==null||fast.next==null){
return false;
}
//快指針比慢指針多一步
slow=slow.next;
fast=fast.next.next;
}
return true;
}
復雜度分析
時間復雜度O(N) : 當鏈表中存在環時,每一輪移動后,快慢指針的距離將減小一。而初始距離為環的長度,因此至多移動 N 輪。
空間復雜度O(1) : 只使用了兩個指針額外的空間
將兩個有序鏈表合并為一個新的有序鏈表并返回。新鏈表是通過拼接給定的兩個鏈表的所有節點組成的。
示例:輸入:1->2->4, 1->3->4 輸出:1->1->2->3->4->4
思路;雙指針思想
public ListNode mergeTwoLists(ListNode l1, ListNode l2) {
if(l1 == null) return l2;
if(l2 == null) return l1;
if(l1.val < l2.val){
l1.next = mergeTwoLists(l1.next,l2);
return l1;
}else{
l2.next = mergeTwoLists(l1,l2.next);
return l2;
}
}
給定一個排序鏈表,刪除所有重復的元素,使得每個元素只出現一次。
示例 1:輸入: 1->1->2 輸出: 1->2
示例 2:輸入: 1->1->2->3->3 輸出: 1->2->3
//一次遍歷,注意邊界條件。
public ListNode deleteDuplicates(ListNode head) { ? ?
ListNode cur = head; ? ?
while(cur != null && cur.next != null){ ? ? ? ?
if(cur.val == cur.next.val) ? ? ? ? ? ?
cur.next = cur.next.next; ? ? ? ?
else ? ? ? ? ? ?
cur = cur.next; ? ?
} ? ?
return head;
}?
給定一個鏈表,刪除鏈表的倒數第 n 個節點,并且返回鏈表的頭結點。
示例:給定一個鏈表: 1->2->3->4->5, 和 n = 2. 當刪除了倒數第二個節點后,鏈表變為 1->2->3->5.
說明:給定的 n 保證是有效的。
//設置啞節點1,讓它走 n+1 步,再設置啞節點2,然后啞節點1和啞節點2一起移動,
//直到啞節點1走完鏈表,此時啞節點1和啞節點2之間正好隔著 n 個節點,再通過啞節點2刪除倒數第 n 個節點。
public ListNode removeNthFromEnd(ListNode head, int n) { ? ?
ListNode dummy = new ListNode(0); ? ?
dummy.next = head; ? ?
ListNode first = dummy; ? ?
for (int i = 1; i <= n + 1;i++){ ? ? ? ?
first = first.next; ? ?
} ? ?
ListNode second = dummy; ? ?
while(first != null){ ? ? ? ?
first = first.next; ? ? ? ?
second = second.next; ? ?
} ? ?
second.next = second.next.next; ? ?
return dummy.next;
}?
給定一個鏈表,兩兩交換其中相鄰的節點,并返回交換后的鏈表。
你不能只是單純的改變節點內部的值,而是需要實際的進行節點交換。
示例:給定 1->2->3->4, 你應該返回 2->1->4->3.
//設置啞節點,注意循環條件,指針移動的速度是2(因為需要兩兩交換節點)。
public ListNode swapPairs (ListNode head) { ? ?
ListNode dummy = new ListNode(-1); ? ?
dummy.next = head; ? ?
ListNode pre = dummy; ? ?
while (pre.next != null && pre.next.next != null) { ? ? ? ?
ListNode l1 = pre.next; ? ? ? ?
ListNode l2 = pre.next.next; ? ? ? ?
l1.next = l2.next; ? ? ? ?
l2.next = l1; ? ? ? ?
pre.next = l2; ? ? ? ?
pre = l1;
? ?} ? ?
return dummy.next;
}?
給定兩個非空鏈表來代表兩個非負整數。數字最高位位于鏈表開始位置。它們的每個節點只存儲單個數字。將這兩數相加會返回一個新的鏈表。
你可以假設除了數字 0 之外,這兩個數字都不會以零開頭。
示例:輸入: (7 -> 2 -> 4 -> 3) + (5 -> 6 -> 4) 輸出: 7 -> 8 -> 0 -> 7
//既然不能改變鏈表的結構(翻轉鏈表),那就用一個棧來保存鏈表中的值,可以做到逆向輸出。
//相加部分的代碼邏輯就按常規思路寫。
public ListNode addTwoNumbers (ListNode l1, ListNode l2) { ? ?
Stack<Integer> l1Stack = listNodetoStack(l1); ? ?
Stack<Integer> l2Stack = listNodetoStack(l2); ? ?
int carry = 0; ? ?
ListNode head = new ListNode(-1); ? ?
while (!l1Stack.isEmpty() || !l2Stack.isEmpty() || carry != 0) { ? ? ? ?
int x = l1Stack.isEmpty() ? 0 : l1Stack.pop(); ? ? ? ?
int y = l2Stack.isEmpty() ? 0 : l2Stack.pop(); ? ? ? ?
int sum = x + y + carry; ? ? ? ?
ListNode node = new ListNode(sum % 10); ? ? ? ?
carry = sum / 10; ? ? ? ?
node.next = head.next; ? ? ? ?
head.next = node; ? ?
} ? ?
return head.next;
}
private Stack<Integer> listNodetoStack (ListNode head) { ? ?
Stack<Integer> stack = new Stack<>(); ? ?
while (head != null) { ? ? ? ?
stack.push(head.val); ? ? ? ?
head = head.next; ? ?
} ? ?
return stack;
}?
給定一個頭結點為 root 的鏈表, 編寫一個函數以將鏈表分隔為 k 個連續的部分。
每部分的長度應該盡可能的相等: 任意兩部分的長度差距不能超過 1,也就是說可能有些部分為 null。
這k個部分應該按照在鏈表中出現的順序進行輸出,并且排在前面的部分的長度應該大于或等于后面的長度。
返回一個符合上述規則的鏈表的列表。
舉例: 1->2->3->4, k = 5 // 5 結果 [ [1], [2], [3], [4], null ]
示例 1:
輸入: root = [1, 2, 3], k = 5 輸出: [[1],[2],[3],[],[]] 解釋: 輸入輸出各部分都應該是鏈表,而不是數組。 例如, 輸入的結點 root 的 val= 1, root.next.val = 2, \root.next.next.val = 3, 且 root.next.next.next = null。 第一個輸出 output[0] 是 output[0].val = 1, output[0].next = null。 最后一個元素 output[4] 為 null, 它代表了最后一個部分為空鏈表。
示例 2:
輸入: root = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10], k = 3 輸出: [[1, 2, 3, 4], [5, 6, 7], [8, 9, 10]] 解釋: 輸入被分成了幾個連續的部分,并且每部分的長度相差不超過1.前面部分的長度大于等于后面部分的長度。
提示:
● root 的長度范圍: [0, 1000].
● 輸入的每個節點的大小范圍:[0, 999].
● k 的取值范圍: [1, 50].
/*思路:先統計出鏈表長度,除以 k, 求商和余數,其中:
● 余數代表最后結果中有多少個長鏈表
● 商代表每個短鏈表的長度(結果集中后部的鏈表)
● 長鏈表比短鏈表多一個節點*/
public ListNode[] splitListToParts (ListNode root, int k) { ? ?
ListNode cur = root; ? ?
int len = 0; ? ?
while (cur != null) { ? ? ? ?
cur = cur.next; ? ? ? ?
len++; ? ?
} ? ?
int mod = len % k; ? ?
int size = len / k; ? ?
cur = root; ? ?
ListNode[] ans = new ListNode[k]; ? ?
for (int i = 0; cur != null && i < k; i++) { ? ? ? ?
ans[i] = cur; ? ? ? ?
int curSize = size + (mod-- > 0 ? 1 : 0); ? ? ? ?
for (int j = 0; j < curSize - 1; j++) { ? ? ? ? ? ?
cur = cur.next; ? ? ? ?
} ? ? ? ?
ListNode next = cur.next; ? ? ? ?
cur.next = null; ? ? ? ?
cur = next; ? ?
} ? ?
return ans;
}?
給定一個單鏈表,把所有的奇數節點和偶數節點分別排在一起。請注意,這里的奇數節點和偶數節點指的是節點編號的奇偶性,而不是節點的值的奇偶性。
請嘗試使用原地算法完成。你的算法的空間復雜度應為 O(1),時間復雜度應為 O(nodes),nodes 為節點總數。
示例 1:輸入: 1->2->3->4->5->NULL 輸出: 1->3->5->2->4->NULL
示例 2:輸入: 2->1->3->5->6->4->7->NULL 輸出: 2->3->6->7->1->5->4->NULL
說明:
● 應當保持奇數節點和偶數節點的相對順序。
● 鏈表的第一個節點視為奇數節點,第二個節點視為偶數節點,以此類推。
設置三個指針,其中奇指針和偶指針是很自然能想到的,evenHead起輔助作用,用于將奇鏈表和偶鏈表結合起來。
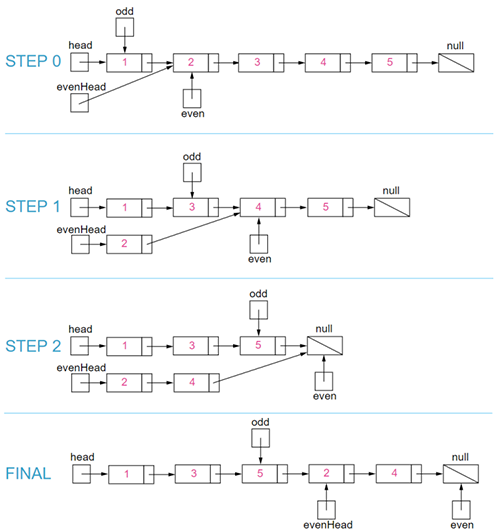
public ListNode oddEvenList (ListNode head) { ? ?
ListNode odd = head; ? ?
ListNode even = head.next; ? ?
ListNode evenHead = even; ? ?
while (even != null && even.next != null) { ? ? ? ?
odd.next = even.next; ? ? ? ?
odd = odd.next;
? ? ? ? even.next = odd.next;
? ? ? ? even = even.next;
? ? }
? ? odd.next = evenHead;
? ? return head;
}
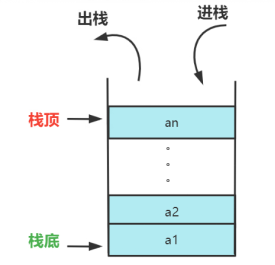
棧是一種后進先出(Last in First Out)的數據結構,簡稱 LIFO。棧是一種特殊的線性表,其只允許在固定的一端進行插入和刪除元素操作。進行數據插入和刪除操作的一端稱為棧頂,另一端稱為棧底。
public static void main(String[] args) {
Stack < Integer > stack = new Stack < Integer > ();
//入棧
stack.push(3); //棧底
stack.push(4);
stack.push(5);
stack.push(7); //棧頂
//出棧:彈出棧頂元素
System.out.println(stack.pop()); //7
//再彈一次,此時棧頂元素為5了,如下。
System.out.println(stack.pop());
//獲取棧頂元素但不刪除,這時的棧頂元素以及是4了
System.out.println(stack.peek());
//判斷棧頂元素是否為空
System.out.println(stack.empty());
Stack < Integer > stack1 = new Stack < > ();
System.out.println(stack1.empty());
//獲取棧中的元素的位置,棧頂為1號,此時stack中有3,4兩個元素,所以4元素的位置為1號
System.out.println(stack.search(4));
//使用父類的方法,stack繼承自Vector
System.out.println(stack.isEmpty());
}
A. 棧頂元素最先能被刪除
B. 棧頂元素最后才能被刪除
C. 棧底元素永遠不能被刪除
D. 棧底元素最先被刪除
答案: A
解析:棧里面的元素都有被刪除的機會,只不過棧頂的元素最先刪除,棧底的元素最后刪除。
A. 2 3 4 1 5
B. 5 4 1 3 2
C. 2 3 1 4 5
D. 1 5 4 3 2
答案: B
解析:B中1比3先進入,所以1在3之后出來。
A. 棧的頂
B. 棧的底
C. 棧指針
D. 棧中的數據
答案: B
解析:暫無解析。
A. 堆區,棧區
B. 常量區,堆區
C. 全局區,棧區
D. 棧區,堆區
答案: A
解析:對象放在堆去,引用放在棧區。
A. SSSSXXXX
B. SSSXXSXX
C. SXSSXXSX
D. SXSXSXSX
答案:D
解析:按照選項中的操作會得到的出棧順序如下
選項A中,abcd進棧,依次出棧,得到出棧順序是dcba;
選項B中,abc進棧,cb出棧,d進棧,da出棧,得到出棧順序是cbda;
選項C中,a進棧,a出棧,bc進棧,cb出棧,d進棧,d出棧,中得到出棧順序是acbd;
選項D中,a進棧,a出棧,b進棧,b出棧,c進棧,c出棧,d進棧,d出棧,中得到出棧順序是abcd;所以正確選項為D。
A. XYZ
B. YZX
C. ZXY
D. ZYX
答案: C
解析:因為棧是先進后出,X在Y之前進入,所以X肯定在Y之后出來,所以ZXY不可能。
class MinStack {
private Stack < Integer > stack;
private Stack < Integer > minStack;
public MinStack() {
stack = new Stack < > ();
minStack = new Stack < > ();
}
public void push(int val) {
stack.push(val);
if (!minStack.empty()) {
int top = minStack.peek();
if (val <= top) {
minStack.push(val);
}
} else {
minStack.push(val);
}
}
public void pop() {
int popVal = stack.pop();
if (!minStack.empty()) {
int top = minStack.peek();
if (top == popVal) {
minStack.pop();
}
}
}
public int top() {
return stack.peek();
}
public int getMin() {
return minStack.peek();
}
}
public class Demo5 {
public static void main(String[] args) {
int[] A = {
1, 2, 3, 4, 5
};
int[] B = {
4, 5, 3, 2, 1
};
System.out.println(IsPopOrder(A, B));
}
public static boolean IsPopOrder(int[] pushA, int[] popA) {
Stack < Integer > stack = new Stack < > ();
int j = 0;
for (int i = 0; i < pushA.length; i++) {
stack.push(pushA[i]);
while (j < popA.length && !stack.empty() && stack.peek() == popA[j]) {
stack.pop();
j++;
}
}
return stack.empty();
}
}
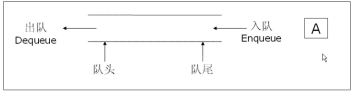
隊列是一種先進先出的數據結構,這和棧有所不同,但又更容易理解。類似于食堂排隊打飯,車站排隊買票。后來的人排在隊伍最后邊,先來的人先打飯或者買票走。
隊列:只允許在一端進行插入數據操作,在另一端進行刪除數據操作的特殊線性表,進行插入操作的一端稱為隊尾 出隊列:進行刪除操作的一端稱為隊頭
A. 1,2,........,n
B. 1,2,4,3,5,6,.....,n
C. n,n-1,....,1
D. 以上均有可能
答案:A
解析:隊列是先進先出,所以B選項中3比4先入隊,所以3比4先出隊;C選項同理。
A. 最早插入隊列中的元素總是最后被刪除
B. 當同時進行插入、刪除操作時,總是插入操作優先
C. 每當有刪除操作時,總是要先做一次插入操作
D. 每次從隊列中刪除的總是最早插入的元素
答案:D
解析:A選項中隊列中的元素不一定非得刪除;
B選項中,插入和刪除的操作看誰先執行就就優先操作;
C選項中,刪除操作時和插入沒有關系;
A.sq.front=(sq.front+1)% maxsize;
B.sq.front=sq.front+1;
C.sq.rear=(sq.rear+1)% maxsize;
D.sq.rear=sq.rear+1;
答案:A
解析:考察的是循環隊列的特性和定義以及操作。 循環隊列:最后一個單元的后繼是第一個單元的隊列。
A.單向隊列在允許刪除的一端叫隊頭,在允許插入的一端叫隊尾。
B.單向隊列在允許刪除的一端叫隊尾,在允許插入的一端叫隊頭。
C.隊列可以用數組實現,也可以用鏈表實現
D.隊列是先進先出的,棧是后進先出的
正確答案:ACD
解析:暫無解析
A.棧是限定只能在表的一端進行插入和刪除操作。
B.隊列是限定只能在表的一端進行插入和在另一端進行刪除操作。
C.棧和隊列都屬于線性表
D.棧的插入操作時間復雜度都是o(1),隊列的插入操作時間復雜度是o(n)
正確答案:D
解析:暫無解析
隊列本身是有序列表,若使用數組的結構來存儲隊列的數據,則隊列數組的聲明如下圖 , 其中 maxSize 是該隊列的最大容量。
因為隊列的輸出、輸入是分別從前后端來處理,因此需要兩個變量 front 及 rear 分別記錄隊列前后端的下標,front 會隨著數據輸出而改變,而 rear 則是隨著數據輸入而改變,如圖所示
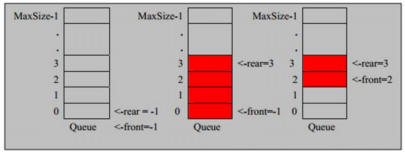
當我們將數據存入隊列時稱為” addQueue ”, addQueue 的處理需要有兩個步驟:思路分析
1)將尾指針往后移: rear+1 , 當 front == rear 【空】
2)若尾指針 rear 小于隊列的最大下標 maxSize-1 ,則將數據存入 rear 所指的數組元素中,否則無法存入數據。rear == maxSize - 1[ 隊列滿 ]
import java.util.Scanner;
public class ArrayQueueDemo {
public static void main(String[] args) {
//測試一把
// 創建一個隊列
ArrayQueue queue = new ArrayQueue(3);
char key = ' '; //接收用戶輸入
Scanner scanner = new Scanner(System.in); //
boolean loop = true;
//輸出一個菜單
while (loop) {
System.out.println("s(show): 顯示隊列");
System.out.println("e(exit): 退出程序");
System.out.println("a(add): 添加數據到隊列");
System.out.println("g(get): 從隊列取出數據");
System.out.println("h(head): 查看隊列頭的數據");
key = scanner.next().charAt(0); //接收一個字符
switch (key) {
case 's':
queue.showQueue();
break;
case 'a':
System.out.println("輸出一個數");
int value = scanner.nextInt();
queue.addQueue(value);
break;
case 'g': //取出數據
try {
int res = queue.getQueue();
System.out.printf("取出的數據是%d\n", res);
} catch (Exception e) {
// TODO: handle exception
System.out.println(e.getMessage());
}
break;
case 'h': //查看隊列頭的數據
try {
int res = queue.headQueue();
System.out.printf("隊列頭的數據是%d\n", res);
} catch (Exception e) {
// TODO: handle exception
System.out.println(e.getMessage());
}
break;
case 'e': //退出
scanner.close();
loop = false;
break;
default:
break;
}
}
System.out.println("程序退出~~");
}
}
class ArrayQueue {
private int maxSize; //表示數組的最大容量
private int front; //表示隊列頭
private int rear; //表示隊列尾
private int[] arr; //該數組用于存放數據,模擬隊列
//創建隊列的構造器
public ArrayQueue(int arrMaxSize) {
maxSize = arrMaxSize;
arr = new int[maxSize];
front = -1; // 指向隊列頭部前一個位置
rear = -1; // 指向隊列尾,指向隊列尾的數據(即就是隊列最后一個數據)
}
//判斷隊列是否滿
public boolean isFull() {
return rear == maxSize - 1;
}
// 判斷隊列是否為空
public boolean isEmpty() {
return rear == front;
}
// 添加數據到隊列
public void addQueue(int n) {
// 判斷隊列是否滿
if (isFull()) {
System.out.println("隊列滿,不能加入數據~");
return;
}
rear++; // 讓 rear 后移
arr[rear] = n;
}
// 獲取隊列的數據, 出隊列
public int getQueue() {
// 判斷隊列是否空
if (isEmpty()) {
// 通過拋出異常
throw new RuntimeException("隊列空,不能取數據");
}
front++; // front 后移
return arr[front];
}
// 顯示隊列的所有數據
public void showQueue() {
// 遍歷
if (isEmpty()) {
System.out.println("隊列空的,沒有數據~~");
return;
}
for (int i = 0; i < arr.length; i++) {
System.out.printf("arr[%d]=%d\n", i, arr[i]);
}
}
// 顯示隊列的頭數據, 注意不是取出數據
public int headQueue() {
// 判斷
if (isEmpty()) {
throw new RuntimeException("隊列空的,沒有數據~~");
}
return arr[front + 1];
}
}
創建一個長度為6的整數數組,數組中有六個整數(直接賦值即可)。遍歷數組中的每個元素,元素之間用空格隔開。比如:
數組為:{1,2,3,4,5}
打印結果:1 2 3 4 5
package com.bjpowernode.array;
/*創建一個長度為6的整數數組,數組中有六個整數(直接賦值即可)。遍歷數組中的每個元素,元素之間用空格隔開。
比如數組為:{1,2,3,4,5}
打印結果:1 2 3 4 5*/
public class Test1 {
public static void main(String[] args) {
int [] arr={1,2,3,4,5};//定義整數類型數組
for(int i=0;i<arr.length;i++){
System.out.print(arr[i]+"\t");
}
}
}
現有一個小數數組{12.9,53.54,75.0,99.1,3.14}。請編寫代碼,找出數組中的最小值并打印。
操作步驟
定義小數類型數組并存入元素。
定義小數變量min代表最小值。
遍歷數組,用每個元素依次和變量min對比。
如果元素小于min,則把元素賦值給min。
遍歷結束之后打印最小值。
package com.bjpowernode.array;
/*
現有一個小數數組{12.9,53.54,75.0,99.1,3.14}。請編寫代碼,找出數組中的最小值并打印。
### 訓練提示
1. 數組的元素是小數,需要定義小數類型數組。
2. 找最小值和找最大值的思路是一樣的。*/
public class Test2 {
public static void main(String[] args) {
double[] arr={12.9,53.54,75.0,99.1,3.14};//定義一個double數組
double min=arr[0];
for(int i=1;i< arr.length;i++){
if(min>arr[i]){
min=arr[i];
}
}
System.out.println("最小值是"+min);
}
}
A. 520
B. 522
C. 524
D. 518
答案:A
解析:a[2][0]和a[1][0]相距10個元素,所以相差4*10=40個字節;
A. 12,18,14,16
B. 12,14, 18,16
C. 6,9,7,8
D. 6,7,9,8
答案:A
解析:這個一維數組A的長度是11。
因此,第一個比較的元素是A[11/2]=A[5]=12;第二個比較的元素是A[(6+11)/2]=A[8]=18;第三個比較的元素是A[(6+7)/2]=A[6]=14;第四個比較的元素是A[(7+7)/2]=A[7]=16。
A. a[0][2*1]
B. a[1][3]
C. a[4-2][0]
D. a[0][2+2]
答案:D
解析:引用的時候是從0下標開始,不能越界。