![]() 二叉樹面試題
二叉樹面試題
樹:樹是由根節點和若干顆子樹構成的。樹是由一個集合以及在該集合上定義的一種關系構成的。集合中的元素稱為樹的節點,所定義的關系稱為父子關系。
二叉樹:樹是由根節點和若干子樹構成的。每個節點最多含有兩個子樹的樹稱為二叉樹。
度:一個結點含有的子樹的個數
葉子節點或終端節點:度為0的節點
節點的層數: 樹根到節點的路徑長度是該節點的層數,節點都有層數,根所在的層為0
樹的高度或深度:樹的高度或深度是樹中節點的最大層數(最長路徑的長度)加1 ,空樹高度為0,只有根節點的樹高度為1。
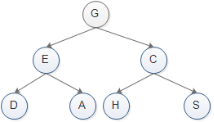
(1)先序遍歷:先訪問根節點,然后訪問左子樹,若當前節點無左子樹,則訪問當前節點的右子樹;
如上圖:
1.訪問該二叉樹的根節點,找到 G;
2.訪問節點 G 的左子樹,找到節點 E;
3.訪問節點 E的左子樹,找到節點 D;
4.由于訪問節點 D左子樹失敗,且也沒有右子樹,因此以節點 D為根節點的子樹遍歷完成。 但節點 E 還沒有遍歷其右子樹,因此現在開始遍歷,即訪問節點 A;
5.由于節點 A 無左右子樹,因此節點 A 遍歷完成,并且由此以節點 E 為根節點的子樹也遍歷完成。現在回到節點 G ,并開始遍歷該節點的右子樹,即訪問節點 C;
6.訪問節點 C 左子樹,找到節點 H;
7.由于節點 H無左右子樹,因此節點 H 遍歷完成,回到節點 C 并遍歷其右子樹,找到節點 S;
8.節點 S 無左右子樹,因此以節點 S為根節點的子樹遍歷完成,同時回歸節點 G。由于節點 G 的左右子樹全部遍歷完成,因此整個二叉樹遍歷完成;
9.最終遍歷的結果就是:GEDACHS
(2)中序遍歷:先訪問左子樹,然后訪問根節點,最后訪問右子樹,即左根右。所以遍歷的結果是:DEAGHCS。
(3)后序遍歷:先訪問左孩子,然后訪問右孩子,最后訪問根節點,即左右根。所以遍歷的結果是:DAEHSCG。
(4)寬度遍歷:從根節點開始依次遍歷左子節點和右子節點,直到所有子節點都變遍歷完為止。所以遍歷的結果是:GECDAHS。
1.前序遍歷的第一個遍歷節點必是根節點,而后序遍歷的最后一個遍歷節點必是根節點;
2.根據中序遍歷順序無法判斷根節點,但若已知根節點,則可根據中序遍歷順序判斷出左子樹的組成元素和右子樹的組成元素;
算法思路:
1.首先通過先序遍歷【GEDACHS】或者后序遍歷【DAEHSCG】可以得到二叉樹的根節點G,通過中序遍歷【DEAGHCS】可以得到左右子樹的成員,即左子樹的成員【DEA】,右子樹的成員是【HCS】。
2.然后將左子樹【DEA】看作新的二叉樹,通過后序遍歷【DAEHSCG】可以得到新二叉樹的根節點為E。又通過中序遍歷【DEAGHCS】可以得到A為E的右子樹,D為E的左子樹。
3.右子樹HCS同理
依此類推,即可畫出整棵二叉樹。不難看出,畫出這棵二叉樹的順序,就是我們想要得到的先序輸出順序,因此我們只需要在畫二叉樹時,對當前根節點進行輸出,即可完成題目需要。這樣只需要設置節點輸出的位置就可以得到對應的遍歷結果。
public class Node {
public int data;
public Node leftChild;
public Node rightChild;
public Node(int data) {
this.data = data;
}
}
public static void OrderTraveral(TreeNode node){
if(node == null){
return;
}
//遞歸前序遍歷 根-> 左-> 右
/*
System.out.print(node.data+" ");
OrderTraveral(node.leftChild);
OrderTraveral(node.rightChild);*/
//遞歸中序遍歷 左-> 根-> 右
/*
OrderTraveral(node.leftChild);
System.out.print(node.data+" ");
OrderTraveral(node.rightChild);*/
//遞歸后序遍歷 左-> 右->根
/*
OrderTraveral(node.leftChild);
OrderTraveral(node.rightChild);
System.out.print(node.data+" ");*/
}
先序的思路:采用棧的先進后出思想進行實現的
1.首先有一個棧s1。
2.先將頭結點入棧s1。
3.頭結點出棧,判斷當前結點的右孩子是不是為空,不為空則入棧;判斷當前結點的左孩子是不是為空不為空則入棧。周而復始依次迭代。
public static void preOrder(Node head) {
System.out.print("pre-order: ");
if (head != null) {
Stack<Node> stack = new Stack<Node>();
stack.add(head);
while (!stack.isEmpty()) {
head = stack.pop();
System.out.print(head.value + " ");
if (head.right != null) {
stack.push(head.right);
}
if (head.left != null) {
stack.push(head.left);
}
}
}
System.out.println();
}
中序的思路:采用棧的先進后出思想進行實現的
1.首先有一個棧s1。
2.判斷頭結點是不是為空,不為空則入棧s1,并獲取頭結點的左節點。如果為空則出棧頭結點,并獲取頭結點的右節點。周而復始依次迭代。
public static void inOrder(Node head) {
System.out.print("in-order: ");
if (head != null) {
Stack<Node> stack = new Stack<Node>();
while (!stack.isEmpty() || head != null) {
if (head != null) {
stack.push(head);
head = head.left;
} else {
head = stack.pop();
System.out.print(head.value + " ");
head = head.right;
}
}
}
System.out.println();
}
后序思路:
1.首先有兩個棧s1和s2
2.先講頭結點入棧s1
3.棧s1的頭結點出棧并入棧s2,判斷當前結點的左孩子是不是為空,不為空則入棧s1;判斷當前結點的右孩子是不是為空不為空則入棧s1。周而復始依次迭代,這樣循環完后s2棧的入棧的順序就是頭右左;
4.將s2彈棧,周而復始依次迭代,彈出的順序為左右頭;
public static void posOrder(Node head) {
System.out.print("pos-order: ");
if (head != null) {
Stack<Node> s1 = new Stack<Node>();
Stack<Node> s2 = new Stack<Node>();
s1.push(head);
while (!s1.isEmpty()) {
head = s1.pop();
s2.push(head);
if (head.left != null) {
s1.push(head.left);
}
if (head.right != null) {
s1.push(head.right);
}
}
while (!s2.isEmpty()) {
System.out.print(s2.pop().value + " ");
}
}
System.out.println();
}
寬度遍歷思路:
1.首先有一個隊列queue1和一個levelMap
2.先講頭結點入隊queue1
3.隊列queue1的頭結點出隊并輸出當前節點,判斷當前結點的左孩子是不是為空,不為空則入隊queue1;判斷當前結點的右孩子是不是為空不為空則入隊queue1。周而復始依次迭代;
public static void width(Node head) {
if(head == null) {
return 0;
}
Queue<Node> queue = new LinkedList<>();
queue.add(head);
while(!queue.isEmpty()) {
Node cur = queue.poll();
System.out.println(cur.value);
if(cur.left!=null) {
queue.add(cur.left);
}
if(cur.right!=null) {
queue.add(cur.right);
}
}
}
思路:
1. 首先有一個隊列queue1,一個levelMap,一個遍歷層數curLevel
2. 先將頭結點入隊queue1,并將頭結點所在的層數存儲到levelMap,一開始頭節點在第一層所以levelMap.put(head, 1);
3. 隊列queue1的頭結點出隊,獲取頭結點所在的層數curNodeLevel ,如果當前節點的層數curNodeLevel 和遍歷的層數levelMap相等,則讓當前層數的節點curLevelNodes自加1,否則就讓遍歷的層數curLevel自加1,并且當前層數的節點curLevelNodes初始化成1,確定最大寬度;判斷當前結點的左孩子是不是為空,不為空則將該左孩子節點所在的層數存儲到levelMap并入隊queue1;判斷當前結點的右孩子是不是為空不為空則將該右孩子節點所在的層數存儲到levelMap入隊queue1。周而復始依次迭代;
public static int w(Node head) {
if (head == null) {
return 0;
}
Queue < Node > queue = new LinkedList < > ();
queue.add(head);
HashMap < Node, Integer > levelMap = new HashMap < > ();
levelMap.put(head, 1);
int curLevel = 1;
int curLevelNodes = 0;
int max = Integer.MIN_VALUE;
while (!queue.isEmpty()) {
Node cur = queue.poll();
int curNodeLevel = levelMap.get(cur);
if (curNodeLevel == curLevel) {
curLevelNodes++;
} else {
max = Math.max(max, curLevelNodes);
curLevel++;
curLevelNodes = 1;
}
if (cur.left != null) {
levelMap.put(cur.left, curNodeLevel + 1);
queue.add(cur.left);
}
if (cur.right != null) {
levelMap.put(cur.right, curNodeLevel + 1);
queue.add(cur.right);
}
}
return max;
}
搜索二叉樹是一種特殊有序的二叉樹,如果一棵樹不為空,并且如果它的根節點左子樹不為空,那么它左子樹上面的所有節點的值都小于它的根節點的值,如果它的右子樹不為空,那么它右子樹任意節點的值都大于他的根節點的值,它的左右子樹也是二叉搜索樹。
由此可見,如果對二叉搜索樹進行中序排列(左中右),那么會得到一個從小到大的序列。
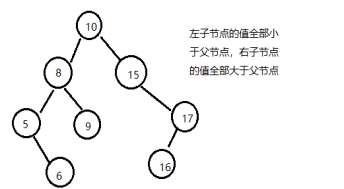
上圖中序排列(左中右)后的順序應該是:5,6,8,9,10,15,16,17。
具體思路:判斷一棵樹是不是搜索二叉樹直接就是看中序遍歷是不是升序,如果是升序就是搜索二叉樹。
public static boolean checkBST2(Node head) {
List<Node> lst=new ArrayList<>();
process(head,lst);
//查看lst的順序是否為升序的即可
}
public static void process(TreeNode head,ListNode lst){
if(node == null){
return;
}
//遞歸中序遍歷 左-> 根-> 右
process(head.leftChild);
lst.add(head);
process(head.rightChild);
}
完全二叉樹是由滿二叉樹而引出來的。對于深度為h 的,有N個結點的二叉樹,當且僅當其每一個結點都與深度為h的滿二叉樹中編號從1至n的結點一一對應時稱之為完全二叉樹。 要注意的是滿二叉樹是一種特殊的完全二叉樹。
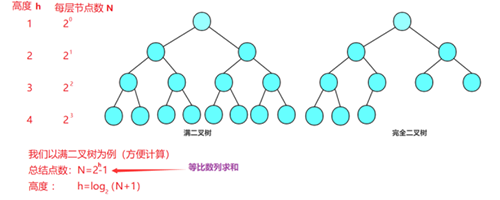
算法思路:
1.首先有一個隊列queue,將頭結點入隊queue,
2.層序遍歷的基礎上,將頭結點出隊,獲取該節點的左孩子和右孩子;
如果該節點的左孩子為空,右孩子不為空則返回false;
如果該節點的左右孩子不全為空,并且該節點不是葉子節點則返回false;
3.如果左孩子不為空,將左孩子入隊;
4.如果右孩子不為空,將右孩子入隊;
5.如果左右孩子都為空,將該節點設置為葉子節點;
6. 【2,3,4,5】步驟周而復始依次迭代;
7.最終返回true或者false;
public static boolean isCBT(Node head) {
if (head == null) {
return true;
}
LinkedList < Node > queue = new LinkedList < > ();
// 是否遇到過左右兩個孩子不雙全的節點
boolean leaf = false;
Node l = null;
Node r = null;
queue.add(head);
while (!queue.isEmpty()) {
head = queue.poll();
l = head.left;
r = head.right;
// 如果遇到了不雙全的節點之后,又發現當前節點不是葉節點
if ((leaf && !(l == null && r == null)) ||(l == null && r != null)) {
return false;
}
if (l != null) {
queue.add(l);
}
if (r != null) {
queue.add(r);
}
if (l == null || r == null) {
leaf = true;
}
}
return true;
}
思路:
1.封裝一個實體類,屬性分別二叉樹和樹的高度。
2.因為拆分后的左子樹和右子樹的情況是一樣的,都是判斷自己的節點個數和樹的高度。采用遞歸的方法獲取樹的節點個數和樹的高度
3.將統計出的最大深度H和節點個數N,看是否滿足N=2H-1。
public static class Info {
public int height;
public int nodes;
public Info(int h, int n) {
height = h;
nodes = n;
}
}
//=========
public static Info full(Node x) {
if (x == null) {
return new Info(0, 0);
}
Info leftData = full(x.left);
Info rightData = full(x.right);
int height = Math.max(leftData.height, rightData.height) + 1;
int nodes = leftData.nodes + rightData.nodes + 1;
return new Info(height, nodes);
}
//===========
public static boolean isF(Node head) {
if (head == null) {
return true;
}
Info data = f(head);
return data.nodes == (1 << data.height - 1);
}
1.任何一個節點的左子樹或者右子樹都是平衡二叉樹。
2.任何一個節點的左子樹高度和右子樹高度差小于等于 1。
1.封裝一個實體類,屬性分別為是不是平衡二叉樹和樹的高度。
public static class ReturnType {??????
public boolean isBalanced;??????
public int height;
??????
public ReturnType(boolean isB, int hei) {?????????
isBalanced = isB;?????????
height = hei;??????
}
}
2.采用遞歸的方法,因為拆分后的左子樹和右子樹的情況是一樣的,都是判斷自己是不是平衡二叉樹和樹的高度,通過判斷各自是不是平衡二叉樹以及計算樹高度差是否小于等于 1。
public static ReturnType process(Node x) {??????
if (x == null) {?????????
return new ReturnType(true, 0);??????
}??????
ReturnType leftData = process(x.left);??????
ReturnType rightData = process(x.right);??????
int height = Math.max(leftData.height, rightData.height) + 1;??????
boolean isBalanced = leftData.isBalanced && rightData.isBalanced && Math.abs(leftData.height - rightData.height) < 2;??????
return new ReturnType(isBalanced, height);???
}
前驅節點:對一棵二叉樹進行中序遍歷,遍歷后的順序,當前節點的前一個節點為該節點的前驅節點;
后繼節點:對一棵二叉樹進行中序遍歷,遍歷后的順序,當前節點的后一個節點為該節點的后繼節點;
下面結構比普通二叉樹節點結構多了一個指向父節點的parent指針。 如何在二叉算樹中找到一節點的后繼節點?
public class Node {
public int value;
public Node left;
public Node right;
public Node parent;
public Node(int val) {
value = val;
}
}
思路:
1.獲取該節點的右子樹。
2.如果右子樹不為空,獲取該右子樹的左子樹,周而復始依次迭代,得到該右子樹的最左邊的節點,該節點就是所求的后繼節點。
public static Node getLeftMost(Node node) {
if (node == null) {
return node;
}
while (node.left != null) {
node = node.left;
}
return node;
}
3.如果右子樹不為空,獲取該節點的父節點,判斷父節點不為空且該節點是不是父節點的左孩子,周而復始依次迭代,如果是左孩子則該父節點就是所求的后繼節點;
public static Node getSuccessorNode(Node node) {
if (node == null) {
return node;
}
if (node.right != null) {
return getLeftMost(node.right);
} else { // 無右子樹
Node parent = node.parent;
while (parent != null && parent.left != node) { // 當前節點是其父親節點右孩子
node = parent;
parent = node.parent;
}
return parent;
}
}